Scripted Supply: A Bitcoin-Based Architecture for EDI and On-Chain Commerce

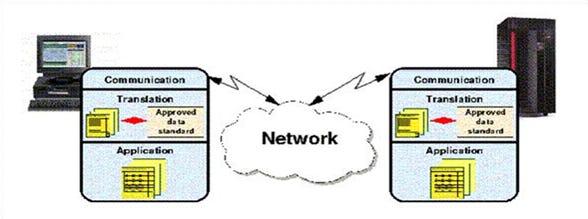
EEI—Electronic Exchange Instructions

Chapter 1: The Problem with EDI and Commerce Today

A Brief History of EDI and Its Evolution

Electronic Data Interchange (EDI), in its canonical form, is the vestigial scaffolding of 20th-century mechanised trade. It represents the fossilised strata of an era in which computation was emergent and decentralised consistency was infeasible. It is often mistaken for a protocol. This is a categorical error. EDI is not a protocol in the formal sense of computability or communication theory. It is an encoding convention, an artefact of standardisation without enforcement—semantics without semantics, structure without determinism, interpretation without validation. It encodes the surface form of intention but not its binding. In computability terms, EDI constitutes a class of languages that are parsed by deterministic finite automata (DFA), but whose interpretation lies outside the model—delegated entirely to human institutions and extra-protocol conventions.

The genesis of EDI lies not in abstraction, but in mechanical necessity. In the late 1960s and early 1970s, commercial entities such as transportation carriers (notably Southern Railway in the US) and automotive manufacturers (notably Ford and General Motors) began to digitise the interchange of commercial forms—purchase orders, invoices, shipping manifests—not by encoding business logic, but by agreeing on fixed record formats. The earliest systems employed fixed-width fields and delimiter-based ASCII templates, operating on the assumption that if sender and receiver agreed on the number of characters per line, then some mutual understanding could be achieved. This principle—syntax as a stand-in for state—persisted as EDI matured.

Two principal standard families dominate the global EDI landscape: ANSI X12 (in North America) and UN/EDIFACT (internationally, under UN auspices). These standards define transaction sets, which are essentially deterministic schema definitions over structured strings. A typical X12 850 purchase order message comprises nested segments (e.g., BEG, REF, N1, PO1) and elements (e.g., product identifiers, quantities, pricing terms) within each segment. These are strictly ordered and bounded by maximal character lengths, yielding a language easily parsed by DFA but not intrinsically meaningful to any executing machine. Parsing is possible. Semantics are not.

Critically, the semantics of EDI are not validated by the machine. That is, a correct EDI message may encode a lie—a document asserting a shipment occurred, payment was made, or goods exist. The protocol does not and cannot prevent this. It contains no enforcement layer. It is this disjunction—between syntactic correctness and semantic truth—that underlies the epistemic instability of all modern commerce built upon EDI.

To demonstrate this formally: let

\(L_{X12}\)

be the set of all syntactically well-formed X12 850 purchase order messages.

\(L_{X12}\)

is regular; a DFA exists that accepts all and only such strings. Let

\( T ⊂ L_{X12}\)

be the subset of messages that correspond to truthful, executed commercial events. There is no algorithm—deterministic or otherwise—within the confines of EDI that can decide membership in T. The mapping from message to reality is extra-formal; it depends on external state, human verification, and exogenous systems (such as delivery scans, payment systems, and legal recourse). This implies that EDI cannot resolve the semantic gap between intent and execution.

As VANs (Value Added Networks) emerged in the 1980s, they became centralised intermediaries responsible for routing and temporarily storing these EDI messages. But VANs offered no guarantees beyond delivery. They are epistemologically passive. They do not and cannot assert that a message corresponds to any real-world change in goods, services, or money. Their primary function was to emulate the postal system, albeit electronically, and with tracking. What they enabled was faster propagation of unverifiable claims. They did not change the trust assumptions—they ossified them.

The advent of XML and later JSON did not alter the fundamental structure. It merely transposed it into human-readable formats. The shift to so-called “modern” APIs (Application Programming Interfaces) in the late 1990s and 2000s—using HTTP, RESTful endpoints, and OAuth-authenticated JSON payloads—did not solve the core problem. APIs, in this context, are merely dynamic interfaces to proprietary EDI schemas. The same semantic impotence remains. Messages are mutable, trust is externalised, and execution is unverifiable. Indeed, APIs have increased opacity, as proprietary implementations may change message behaviour depending on system version, business rules, or vendor configurations. The epistemological question—Did the thing that was declared actually happen?—remains unanswerable within the system.

This is more than a technical deficiency. It is a systemic economic pathology. EDI assumes and institutionalises epistemic fragmentation: each participant in the supply chain maintains its own copy of reality, reconciled periodically through reports, audits, disputes, and litigation. In formal terms, commercial state is non-singular. Let

\(P = {p_1, p_2, ..., p_n} \)

be a set of commercial participants. Each participant

\(p_i\)

maintains a local state

\( σ_i \)

derived from its own ledger and message log. There is no function f such that

\(f(σ_1, σ_2, ..., σ_n) = σ_{consensus}\)

without invoking trust, reconciliation, or external dispute mechanisms. The system lacks state convergence.

This is the critical insight: EDI does not fail when it transmits incorrect information. It fails when it successfully transmits well-formed lies. The system is so formally weak that its correctness criteria are entirely syntactic. One cannot prove execution, only encoding.

Thus, we must discard the illusion that EDI ever provided a deterministic commercial protocol. It is not a mechanism of truth, but a mechanism of expression—frozen at the level of syntactic legibility. It relies on trust, institutions, duplicated accounting, and a universe of human oversight. And because of this, it necessarily entails overhead, delay, redundancy, and error.

In the coming sections, we will demonstrate that the correct formulation of a commercial protocol is not one which encodes documents, but one which encodes state transitions. Each transition must be provable, irreversible, and bound to cryptographic identity and time. Each transition must encode a change in the world—not a declaration of intent. A protocol must enforce the act, not describe it. And for that, one does not need XML. One needs a ledger—a machine of state. Bitcoin, with its Script system, provides exactly that. But before we can build this system, we must finish dismantling the legacy it is to replace.

The Centralisation Problem in EDI Infrastructure

At the heart of every legacy EDI system is a contradiction: it is presented as a machine protocol, yet it presupposes the existence of a trusted intermediary. Despite the deterministic formatting of X12 segments or EDIFACT hierarchies, the transmission of data and its receipt is entirely dependent on a central conduit—one that introduces a control surface, a failure point, and most importantly, a single vector for epistemic manipulation. This centralisation—both technical and institutional—is not a side effect. It is the prerequisite for EDI to function at all. The system cannot operate without assumed custody over message flows.

To understand this fully, we must distinguish between message-based systems and state-based systems. A message-based system encodes an instruction or declaration. It says, “I sent an invoice,” “I acknowledge shipment,” or “Here is a purchase order.” A state-based system does not merely encode that a message was sent—it encodes that a fact has occurred. In formal systems theory, a message carries intended meaning, but a state transition carries executional proof. EDI remains irrevocably message-based. Its semantics are only enforceable through external, off-protocol processes.

The conduit for such messages—whether a Value-Added Network (VAN), an API gateway, or a cloud EDI integration provider—holds the functional position of a semi-trusted relay. These intermediaries are responsible for routing messages, logging them for later access, and in some cases applying validation schemas. But the validation is syntactic. It does not and cannot reach into the domain of semantic or executional truth. A VAN will flag a malformed 810 invoice if the segment count is invalid, or if a data field exceeds its character length. It will not—and cannot—detect a fraudulent claim of delivery, or an inflated billing quantity, or a shipment that never occurred. The centrality of the VAN gives it visibility, but not verification power.

Let us make this precise. Assume a VAN V intermediates messages between sender A and receiver B. Let m be a message asserting a commercial fact ϕ (e.g., that goods were shipped). The VAN V can confirm that message m conforms to a format F, i.e.,

  V ⊨ m ∈ F

However, V cannot confirm the truth of ϕ; that is,

  V ⊭ ϕ

Worse, the recipient B is now in a position of having to either accept or challenge ϕ, but does so on the basis of syntactically valid yet semantically unsubstantiated information. This is not a bug — it is the design.

Moreover, the position of the VAN or intermediary API provider introduces asymmetry into commercial systems. Whoever controls the message relay infrastructure has the ability to:

1. Delay or reorder messages

2. Omit or suppress messages

3. Modify message payloads prior to storage or re-transmission

4. Create audit trails that reflect events that did not occur, or obscure those that did

These are not hypothetical. Real-world supply chains routinely suffer from disputes involving message non-delivery, re-routing through faulty VAN configurations, and API-level race conditions that overwrite or invalidate previously submitted records. No cryptographic guarantees exist at the EDI protocol level. Message mutability is intrinsic. There is no hash-based immutability, no proof-of-inclusion, no timestamping resistant to rollback. The VAN acts as both source and sink of commercial truth, and truth becomes negotiable.

Additionally, centralisation introduces fragility in systemic availability. If the VAN goes offline, no messages are processed. If the API authentication token is revoked—due to expiry, error, or malice—the sender becomes epistemologically silent, regardless of what events are happening in the real world. Worse still, many commercial entities outsource the management of their EDI pipelines to third-party integrators who build custom logic on top of EDI wrappers. These black-box systems collapse transparency and further distance the commercial actor from the structure and semantics of their own messages.

To tie this to formal systems theory: in a centralised EDI infrastructure, the protocol is not closed under composition. While individual messages may be formatted correctly, the system as a whole cannot be composed into a provable state machine.

To tie this to formal systems theory: in a centralised EDI infrastructure, the protocol is not closed under composition. While individual messages may be formatted correctly, the system as a whole cannot be composed into a provable state machine.

Let
  M = m₁, m₂, …, mₖ
be a sequence of valid messages (e.g., 850, 940, 810). There exists no deterministic transition function
  δ
such that:
  σₖ₊₁ = δ(σₖ, mₖ)

where
  σₖ is a well-defined commercial state at step k, and
  σₖ₊₁ is its intended successor.

In other words, there is no formalism by which the reception and syntactic validation of an EDI message leads to an enforced, convergent commercial outcome. The protocol lacks referential transparency — the property that the output of a function is determined solely by its inputs, without side effects or hidden context.

This is a fundamental limitation that cannot be patched by adding more APIs or integrating more cloud systems. As long as state is reconstructed from messages, and those messages are mutable, unverifiable, and interpreted by external systems, the system will always be vulnerable to:

• Epistemic divergence between actors

• Disputes that require institutional arbitration

• Exploits based on timing, message duplication, or race conditions

• Irrecoverable errors due to corrupted state that cannot be rolled back or proven

This centralisation is not merely architectural. It is economic. Intermediaries are not neutral. They monetise position. VANs charge for throughput. API providers charge per request. EDI cloud platforms charge for integration and lock-in. All of them benefit from the friction they allege to reduce. They have no incentive to make state machine transitions deterministic, because their profit model depends on interpretive opacity and the associated need for human dispute resolution, managed services, and institutional enforcement mechanisms.

In the paradigm we are constructing, these problems are not mitigated—they are obliterated. The replacement for EDI is not a better message bus. It is the complete inversion of the model: from message-based to state-based, from centralised to cryptographically enforced, from mutable logs to immutable transitions, from third-party adjudication to machine-enforced commercial fact.

What this requires is not new networking infrastructure. It requires a ledger. Not a ledger in the superficial sense of a database, but in the rigorous sense of an immutable, cryptographically-verifiable, time-ordered structure of state transitions—where each state is both public and self-enforcing. Each transaction must not declare what is believed to have occurred, but must cause it to occur, unambiguously and irreversibly. And for that, only one model exists: a distributed, permissionless ledger governed by an execution language constrained to determinism. This is what Bitcoin, and only Bitcoin Script in its original form, makes possible.

But before we arrive at construction, we must continue excavation. The pathology runs deeper. In the following sections, we will turn our attention to the false promise of API modernisation and the structural decoupling of money from messages—a flaw that EDI will never solve, but Script will never allow.

Why Cloud APIs Are Not a Solution

The modernisation of legacy EDI infrastructures via RESTful APIs, JSON schemas, and cloud-native services is not a transformation of paradigm, but a superficial restructuring of syntax. The illusion is semantic progression; the reality is a more fragile, mutable, and centralised system—merely faster in propagation and more obscured in architecture. The transition from fixed-width ANSI X12 or EDIFACT segments to JSON payloads wrapped in HTTPS endpoints represents an aesthetic improvement, not a semantic one. It does not solve the fundamental computational problem: the absence of binding between declaration and execution.

Cloud APIs do not create state. They return strings. At best, they represent stateless, parameterised function calls over a mutably defined internal model. A call to POST /invoices does not encode the creation of a commercial fact. It triggers a code path that inserts a row into a private database, subject to permission logic, internal validations, and business rule abstractions—all of which are opaque, mutable, and entirely under the control of the API provider. The truth of the invoice—that it exists, that it was sent, that it represents a claim upon a counterparty—is not verifiable outside of the system. In no meaningful sense is it cryptographically proven or externally composable.

Consider the semantic structure of an API transaction:

POST /invoice

 {

  "invoice_id": "12345",

  "amount": "10000",

  "currency": "USD",

  "recipient_id": "XYZ_CORP",

  "due_date": "2025-07-01"

 }

This message is not deterministic in outcome. Its processing depends on mutable logic—stored procedures, cloud function triggers, application state, and authentication context. There is no guarantee that the same payload submitted tomorrow will produce the same effect. Even if the endpoint is idempotent, the invocation is not provable. There is no proof that it happened. There is no proof of what the internal logic returned. There is no commitment to a global, immutable state. In computability terms, the system is not referentially transparent: calling the same function with the same parameters may yield different side effects depending on system state and temporal context.

To formalise the contrast, let f : M → S be the API’s internal mapping from a message  m ∈ M to a state transition s ∈ S.

In legacy EDI and modern API systems, f is undocumented, mutable, and non-verifiable. There exists no external observer that can assert the existence or correctness of f, nor its immutability.

In Bitcoin, by contrast, state transitions are defined as T : σₖ → σₖ₊₁ where σₖ₊₁ is provably derived from σₖ via transaction t, and t is globally published and irreversibly mined into a chain with economic cost.

No such enforcement mechanism exists in cloud APIs.

Furthermore, APIs imply a delegation of truth. The client sends a message. The server responds with a success code—200 OK. The assumption is that the action requested has been completed. But this is merely a trust statement. The server could be compromised. The logic could be flawed. The request could be accepted and then rolled back. The API could respond falsely to preserve business logic continuity. There is no signature. No merkle root. No state commitment.

This is not conjecture. Every API-based SaaS product today allows retroactive modification of state. Invoices can be deleted. Purchase orders edited. Fulfilment logs overwritten. Nothing is cryptographically enforced. Even with “audit logs,” these are mutable constructs—append-only in interface, not in enforcement. They exist at the mercy of administrators and cloud operators.

Additionally, these systems instantiate centralised legal risk. The API provider is often a counterparty to the message itself. Shopify, Oracle Netsuite, SAP Ariba—these platforms not only host but authoritatively interpret the meaning of the messages sent. This means they hold the dual role of ledger maintainer and ledger editor. They are not neutral parties. They are liable to policy shifts, downtime, platform sunsets, feature deprecation, and financial prioritisation of larger clients.

From the perspective of distributed systems, the model violates every constraint of Byzantine fault-tolerant design. There is a single point of failure, a single point of trust, and a single point of authority. From the perspective of programming language theory, the model fails to meet functional purity: side effects dominate, and there is no mathematical mapping from input to output.

Let us formalise this. Suppose P(x) is a payment initiation function over message x, and Q(y) is a delivery confirmation predicate over response y. In current API ecosystems, there exists no proof that P(x) occurred other than the system’s internal logs. There exists no proof that Q(y) corresponds to a legitimate delivery confirmation. There is no canonical external function H such that:

\(H(P(x)) = y \land Q(y) = \text{true} \Rightarrow \text{"Delivery and payment occurred"}\)

In contrast, in a Bitcoin-based transactional model, x is a transaction script, y is a mined output, and Q(y) is verifiable by all nodes globally. P(x) cannot lie because its execution is its truth. The entire logic is executed under a common, deterministic virtual machine, and no party can arbitrarily mutate H. Bitcoin’s H is the proof-of-work enforced ledger history.

Therefore, the introduction of cloud APIs into EDI pipelines does not mitigate trust—it concentrates it. It increases speed while decreasing transparency. It amplifies throughput while collapsing auditability. It creates velocity without verification. It is a system of messages, not state. Of mutable declarations, not enforced facts.

This is not a modernisation. It is a trapdoor. And like all trapdoors in computation, it creates undecidable systems masquerading as deterministic ones. In this environment, no truth exists outside the platform operator’s logs. And if truth is negotiable, then commerce is not programmable. It is litigated.

The goal of EDI was to mechanise commerce. The result was mechanised ambiguity. The goal of cloud APIs was to accelerate trade. The result was accelerated opacity. If we seek a system of commercial certainty—of state, not supposition—we must exit the architecture entirely. APIs are not the road to trustlessness. They are its last, fragile remnant before collapse.

In the next section, we will expose the most severe failure of all: the total disconnection between message and payment. The problem is not simply semantic. It is ontological. Commerce without atomic payment is not commerce—it is correspondence.

Payments and Settlement Remain Detached

No matter how refined the schema, how compliant the message formatting, or how rapid the delivery of a purchase order or invoice, the Electronic Data Interchange system—both in its legacy and modernised forms—fails where it matters most: at the point of payment. The crucial act of commercial finality, the discharge of obligation through transfer of value, exists entirely outside the EDI protocol. There is no binding between message and money. There is no cryptographic, atomic link between invoice and remittance, between delivery and settlement. EDI describes transactions. It does not execute them. It cannot.

Let us formalise the gap. Let m be an EDI message representing a commercial intention (e.g. an 850 purchase order or an 810 invoice). Let p be a payment operation in a separate financial network (e.g. SWIFT, SEPA, ACH, FPS, or VisaNet). There exists no function f: m ↦ p such that f is injective, verifiable, and immutable. In practice, the linkage between m and p is implemented by external metadata: invoice numbers in bank remittance fields, references typed by accounts payable staff, or matching line items in monthly reconciliation spreadsheets. These are not bindings. They are conventions. They are hopeful correlations, not guaranteed constructions.

From a systems architecture perspective, this represents asynchronous, non-atomic protocol bifurcation. Two systems—one for messaging (EDI, ERP, email, API) and one for value transfer (banking, card, crypto)—run in parallel, without enforced consistency.

Let ℳ denote the message domain and ℙ the payment domain. Then for any m ∈ ℳ, there is no guarantee that a corresponding p ∈ ℙ exists, nor that such correspondence can be proven within ℳ. The two domains are not commensurable.

This is a systemic failure, not merely a technical inconvenience. It creates the need for entire industries: invoice factoring, dispute resolution, auditing, chargeback management, legal enforcement, and regulatory compliance. All exist to address the fact that the commercial world cannot prove that payment corresponded to agreement, or that goods matched remittance, or that intention was followed by execution. This is not redundancy. It is parasitism on a defective substrate.

Consider a simple transaction. A supplier issues an invoice for $10,000, payable in 30 days. The invoice is transmitted via EDI as a formatted message. The customer, using separate systems, remits payment via bank wire, noting the invoice number in a reference field. There is no machine-verifiable binding between the invoice message and the value transfer. The systems can diverge. The payment may be delayed, short-paid, misrouted, or posted to the wrong account. The only recourse is human reconciliation and institutional trust.

In Bitcoin, this gap does not exist. The transaction is the payment. The output is the settlement. The script is the agreement. The block is the proof. In other words, the act of committing data to the ledger is the transfer of value. Let t be a Bitcoin transaction and s a locking script representing commercial terms. Then t commits to s and transfers value under those conditions. There is no need for a second system. The transaction itself encodes the truth of the act.

Moreover, Bitcoin enables atomicity. The value and the condition are bound. One cannot occur without the other. The payment is conditional on script satisfaction, and the script execution is conditional on payment being included in the transaction. Formally, let t = (v, s) be a tuple of value v and script s. Then the transaction is valid if and only if s executes successfully and transfers v under the consensus rules. This is a symmetry EDI can never achieve.

The implication is severe: EDI does not mechanise commerce. It mechanises correspondence about commerce. Payment, the sine qua non of transaction finality, is wholly outside its domain. And where payment is not embedded, fraud is always possible. Delay is always possible. Reversal, misrepresentation, denial—these are not edge cases. They are systemic characteristics of all architectures in which payment and promise are not co-located in a single, verifiable state transition.

It is not enough to improve payment APIs. To close the gap, commerce must be implemented as atomic transitions: one state to another, through a deterministic protocol, with value movement and condition enforcement encoded in the same construct. This is what Bitcoin transactions are, and what no other commercial system provides.

Until payment and message are one, commerce remains unverifiable. Until execution and declaration are fused, automation is theatre. EDI without atomicity is performance, not proof. Bitcoin ends that performance. It replaces it with computation.

Failure Modes in Traditional Commercial Systems

One of the most significant flaws in legacy EDI and order management systems lies not in their interfaces, nor in their messaging latency, but in the structural ambiguity that arises from asynchronous processes with mutable, loosely coupled records. The following detailed analysis is prompted by a user-submitted failure case (reproduced visually above) which reveals a class of faults stemming from the decoupling of order state from verifiable logic. These scenarios, far from being fringe, represent systemic vulnerabilities inherent to the "old system" model. Here, we provide a categorical breakdown.

I. Receipt Without Reconciliation — Double Fulfilment Through Document Drift

In the example presented, a customer places an order. The order is processed and an invoice is issued. Before fulfilment is complete, the customer requests an amendment. The office cancels the invoice, but fails to cancel or recall the fulfilment instructions. The warehouse picks and stages the original order. Then, the amended order is processed and picked again. No system detects the duplication. Both packages are staged. The customer collects both, pays only for one, and the company incurs a silent loss.

Root causes:

• Cancellation event not atomically linked to fulfilment state

• Physical goods prepared based on stale logical instructions

• Lack of traceable audit at the staging interface

• Duplicate authorisations without cross-check against amended state

II. State Fragmentation — When Documents Disagree and No Component Knows All

Traditional systems separate logical components: ordering, invoicing, warehousing, collection. Each is driven by mutable representations of the order: form IDs, timestamps, notes. The system presumes coordination, but no shared truth exists. The warehouse does not verify against the live billing system. The office cancels the invoice, but that act exists only in one subsystem. The result: a de-synchronised set of beliefs about what the order “is”.

Failure vector:

• Logical view of order not cryptographically linked across all subsystems

• Multiple valid but non-identical “versions” of the same order

• Authority to fulfil persists without authoritative linkage to billing

---

III. Physical Theft by Protocol Design — Unintentional Overdelivery

In the failure scenario, the customer collects both orders — one intended, one erroneously reissued — and no one challenges this. This is not theft in the legal sense, but loss through protocol misalignment. The system permits overdelivery by design because it has no way to bind pickup to a singular, validated delivery event. There is no enforcement of one-for-one mapping between invoice settlement and physical release.

Contrast with BSV approach:

• In Bitcoin, a transaction to release goods can be cryptographically bound to a single claim

• Each pickup requires proof of settlement or fulfilment via script conditions

• Redundant claims can be made, but only one can be executed on-chain, enforced by UTXO uniquenessIV. Hidden Losses and Delayed Discovery — Stock Drift Detected Only Post Facto

The final consequence is subtle but devastating: the business doesn’t notice the error until a physical stocktake or a manual audit uncovers the discrepancy. This is due to the non-finality of state transitions. There is no “closing event” that says this stock has left and was paid for. Instead, there are fragments: a picked order, a cancelled invoice, a missing audit, and a customer long gone.

Systemic issue:

• No single, irreducible record binding payment and delivery

• Logging happens in documents, not proofs

• Reconciliation is post hoc, not preventative

• Losses are not discovered when they occur, but when the gap is noticed

V. Generalising the Failure Class — Asynchronous Invalidated Authorisations

The failure case exemplifies a broader category: authorisation drift. An event occurs (invoice cancellation) which should invalidate a previous authorisation (warehouse pick). But the system lacks the atomicity or binding condition to enforce this. The result is that old authorisations remain "live", even after they should be void.

Correct model:

• Authorisation is a state function of prior events

• Cancellation must revoke fulfilment not by instruction, but by contractual invalidation

• State machines must evaluate spending conditions at the point of execution, not at point of issue

VI. BSV Remedy: Cryptographic State Binding with Forward-Only Logic

In BSV, this class of error is structurally impossible when systems are designed correctly. Every UTXO (unspent transaction output) is:

• Singular: it can be spent only once

• Conditional: it defines the full script for spendability

• Deterministic: its spend is validated before acceptance

• Immutable: once conditions are set, they cannot be reversed

A warehouse-issued delivery token can be modelled as a UTXO requiring:

• Proof of payment (signature + preimage)

• Time window (optional)

• Destination confirmation (multi-party signing or hash-locked precommitment)

Once a delivery token is claimed, it is spent. The physical act of pickup is linked to this claim. Any other previously staged tokens — even if they physically exist — are logically inert unless validated. Thus, even if two packages are prepared, only one can be collected through valid proof. The other, if claimed, fails consensus validation. No system will recognise the second pickup as legitimate.

---

VII. Conclusion: Designing for Irreversibility Prevents Ambiguity

This failure scenario, while specific, exemplifies a design pattern: systems that treat process steps as mutable messages invite ambiguity. But when each step is a verifiable commitment, state is preserved without contradiction. The role of BSV is not to send instructions. It is to encode proofs of fact. No action is permitted unless its conditions are proven. And no proof can be re-used.

The lesson: avoid state drift by making every action a scriptually bound transition. Model your supply chain as a sequence of spendable rights, not a set of mutable instructions. And ensure that once something is cancelled, it becomes — cryptographically and finally — unspendable. That is how Bitcoin prevents fraud, even in the most mundane corner of the warehouse floor.

The Problem of Redundancy and Verification

The structural flaw of all EDI systems—legacy, API-based, or hybrid—is that each participant maintains their own copy of truth. Not merely their own record, but their own interpretation of what is true. This results in a condition of epistemic fragmentation, where no single source of state is authoritative, and every assertion must be independently verified, reconciled, or disputed. It is not simply that truth is decentralised. It is that truth is duplicated, divergent, and ultimately unverifiable without costly human coordination.

Formally, let

\(P = \{ p_1, p_2, \ldots, p_n \}\)

represent a set of commercial entities participating in a supply chain or transaction network. Each participant pip_ipi​ maintains a local state σi\sigma_iσi​, comprising documents, messages, and ledger entries that reflect their belief about current commercial conditions—inventory, payment status, delivery confirmation, and so on. These local states are constructed from received EDI messages, internal data entry, and manual adjustments. The problem is: for any pair (σi,σj)(\sigma_i, \sigma_j)(σi​,σj​), there is no guarantee of consistency. There is no canonical mapping or consensus function

\(f(σ_1​,…,σ_n​)=σ∗\)

that yields a unified global state. Hence, the system is non-convergent.

This non-convergence introduces three endemic classes of failure:

1. Redundancy of storage and computation: Every party stores every document and every transaction. Purchase orders, invoices, advance shipping notices (ASNs), and remittance advices are duplicated across dozens of systems. Let d∈Dbe a document shared between k parties. Then system-wide storage is at least O(k). This is not merely inefficient—it increases the probability of inconsistency. Data rot, version mismatch, partial updates, and time-dependent interpretations all emerge from the act of redundant storage.

2. Ambiguity of verification: The existence of a message does not prove its correctness. For example, receiving an 810 invoice does not confirm that the goods were received or that the price is correct. Verification is externalised to human processes—phone calls, email chains, quarterly audits. No script enforces semantic truth. All verification is retrospective.

3. Delays from consensus simulation: Because there is no shared ledger, commercial actors simulate agreement through reconciliation cycles. These cycles—weekly, monthly, quarterly—attempt to converge divergent local states through labour. The cost is latency, dispute resolution, and financial misallocation. This is a simulation of consensus, not actual consensus.

Let us illustrate this with a simple example: A purchase order is sent by Company A to Company B. Company B ships the goods, generates an invoice, and posts the expected delivery. Company A logs the expected delivery, updates internal inventory projections, and schedules payment. But the goods are delayed. Or misdelivered. Or underdelivered. Or invoiced incorrectly. Or marked as delivered erroneously. Every system now diverges. Each believes something different about the state of the transaction. And there is no machine-verifiable way to determine who is correct.

In such a system, truth is negotiated, not computed. The participants engage in interpretive reconciliation. Internal records are corrected. Adjustments are made. Exceptions are logged. The result is a system in which the most authoritative truth is the one with the best paper trail, not the best logic.

Contrast this with a model where each commercial event is a state transition encoded in an immutable ledger, and each state change is provable by all parties. Let

\(\sigma_k\)

​ be the current state, and let ttt be a transaction such that

\(\sigma_{k+1} = t(\sigma_k)\)

. In Bitcoin, each ttt is globally broadcast, irreversibly committed, and cryptographically linked to the prior state. No duplication exists. No reconciliation is required. The ledger itself is the authoritative source. Verification is not interpretive—it is algorithmic. It is computation, not conversation.

This eradicates redundancy. There is no need for parallel databases. No need for matching documents. No need for reconciliation meetings. The output of each valid transaction is the input for the next. Every state is derived, not declared.

More precisely: If a party claims a commercial fact ϕ, they must commit to a transaction ttt such that t⊢ϕ and t is publicly visible and mined into a shared ledger. This construct ensures that all claimed facts are not just asserted—they are executed.

Legacy systems lack this. They rely on coordination, and every act of coordination implies both cost and failure risk. In computational terms, they simulate distributed consensus through asynchronous message passing with no Byzantine guarantees and no shared clock. In Bitcoin, consensus is embedded in the protocol: nodes verify, miners enforce, and economic incentives secure the state. This is not simulated reconciliation. It is native finality.

The legacy model breeds redundancy. Bitcoin Script annihilates it. The former distributes data and asks for trust. The latter distributes truth and asks only for computation. Until commerce adopts a model in which all participants compute over the same canonical state, it will remain fragmented, redundant, and vulnerable to falsification masquerading as formality.

Case Study: Shipment Verification Failure

To understand the structural fragility of EDI in practice, one need not speculate. A concrete example—drawn from the lived and routine failures of global logistics—illustrates how an apparently well-functioning EDI pipeline can produce cascading epistemic breakdown. The failure is not one of communication delay or technical malfunction, but of architectural insufficiency: the system cannot represent truth, only messages. These messages may be well-formed, timely, even authenticated. But they are not binding. They do not enforce action. And because they cannot verify execution, they offer no guarantee that what was declared actually happened.

Let us examine a standard multi-stage trade event between two entities: AlphaCorp (buyer) and BetaLogistics (supplier and shipper). Assume both firms are EDI-compliant, ISO-certified, and utilise integrated ERP systems. The following event chain unfolds:

1. Purchase Order Generation: AlphaCorp issues a purchase order (PO), encoded as an ANSI X12 850 message. This message contains line items, quantities, delivery instructions, and terms. The message is valid, timestamped, transmitted via VAN, and logged in both parties’ systems. At this point, a commercial intention is created, but no state change is yet enforced.

2. Acknowledgement: BetaLogistics replies with an 855 Purchase Order Acknowledgement. The message is parsed, validated, and filed. At this point, both systems record agreement on what is to be shipped. Still, no goods have moved, and no value has transferred.

3. Shipment Creation: Upon internal warehouse picking, BetaLogistics generates an 856 Advance Shipping Notice (ASN), which is transmitted to AlphaCorp and accepted without error. The ASN includes serialised packaging, estimated arrival, carrier metadata, and product identifiers. Crucially, the ASN claims that the items have been physically dispatched.

4. Goods in Transit: The shipment is delayed due to rerouting and arrives three days late. During transit, no real-time tracking is integrated into the EDI messages. The system continues to assert that delivery is "pending" on the scheduled date. No update is pushed unless manually triggered.

5. Goods Receipt: At the receiving dock, AlphaCorp discovers that 2 of the 10 pallets are damaged and 1 is missing. However, the receiving system is unable to reject the ASN. Instead, warehouse personnel generate a manual exception report and attach it as a 940 Warehouse Shipping Order Exception—outside the EDI loop. The core EDI system is unaware of the discrepancy.

6. Invoice Issuance: Meanwhile, BetaLogistics generates an 810 Invoice for the full order. The invoice is auto-posted into AlphaCorp’s accounts payable system based on ASN matching, not physical inspection. Payment is scheduled within seven days.

7. Payment Release: The payment is released via a separate financial system with no linkage to EDI except an invoice number typed in a bank reference field. The value transfers. No script, message, or program enforced that the delivery matched the invoice or that the goods were intact.

8. Dispute: Upon quarterly audit, the discrepancy is discovered. AlphaCorp initiates a chargeback request, citing invoice overpayment. BetaLogistics disputes the claim, citing ASN match and confirmed invoice acceptance. The process enters litigation.

From a systems perspective, the problem is this: every step succeeded—in the sense that every EDI message was parsed correctly, transmitted successfully, and logged faithfully. But the system cannot prove anything. It cannot prove that the goods were shipped, only that a message claimed they were. It cannot prove that delivery occurred, only that it was scheduled. It cannot prove that the payment was for delivered goods, only that the amount matched an invoice tied to a message, not an outcome.

Formally, let:

• m_{ship} be the ASN message stating shipment occurred,

• m_{invoice} be the invoice message asserting payment is due,

• p be the payment transaction executed outside the protocol.

There exists no function f such that:

\(f(m_{ship}, m_{invoice}, p) = \phi\)

where ϕ asserts "payment corresponds to received goods under agreed conditions." No such f exists because the elements are non-binding. The payment is not conditional on receipt. The invoice is not conditional on delivery verification. The shipment message is not cryptographically committed to the actual delivery contents.

Had the transaction occurred on-chain using Bitcoin Script, each condition could have been enforced:

• Shipment assertion encoded in a script requiring a delivery proof signature from AlphaCorp.

• Invoice enforced as a script with output spendable only after delivery confirmation.

• Payment encoded as a transaction with a conditional OP_CHECKSIGVERIFY from the recipient, preceded by OP_IF that branches based on delivery hash match.

In such a system, partial deliveries could result in partial payments, and any deviation would result in funds being unspendable, or rerouted to an escrow or dispute branch. The discrepancy would be visible not in audit, but at the moment of transaction execution.

The EDI system succeeded in message handling. It failed in commerce. Because EDI cannot express execution. It can only express expectation. And expectation, no matter how well-formatted, is not truth. Only execution is. Only state is. Only commitment is. Bitcoin encodes commitment.

EDI encodes hope.

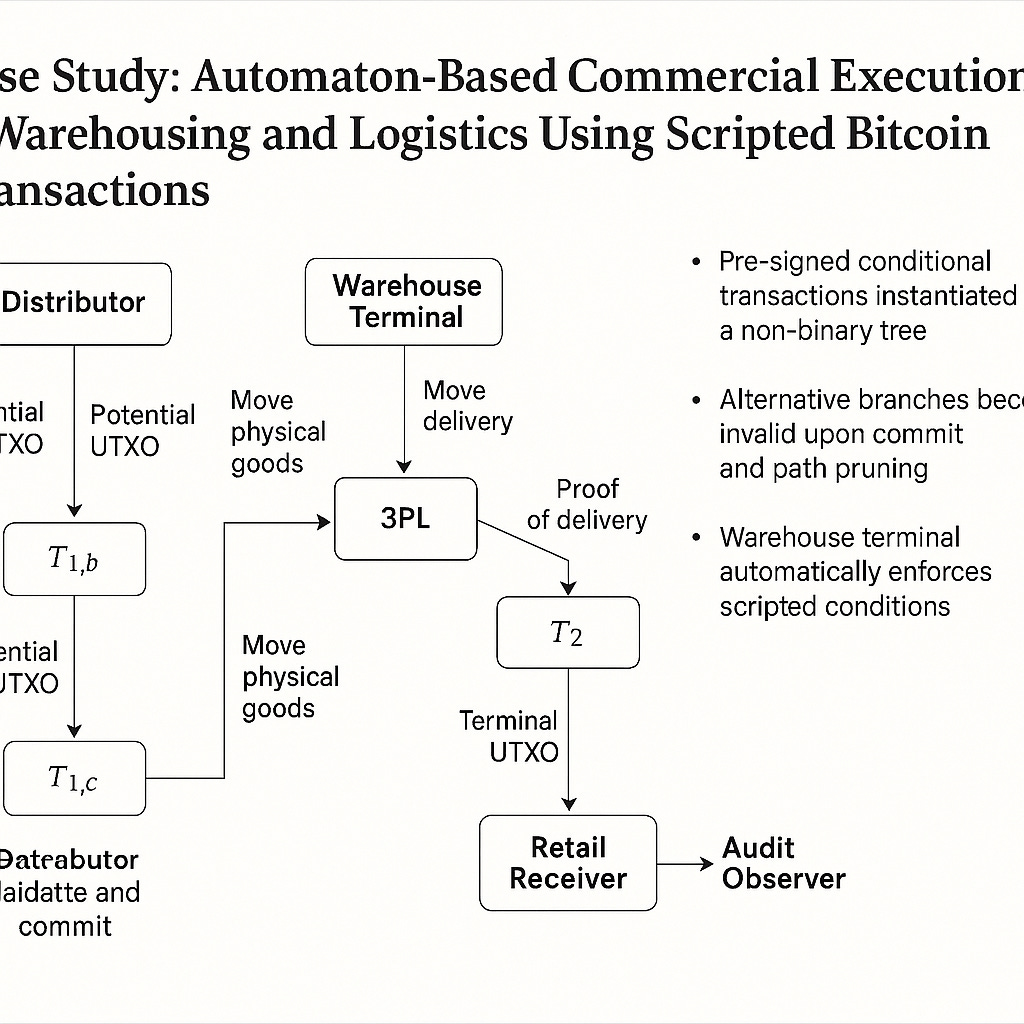
Binding Physical and Logical Infrastructure via Blockchain-State Anchoring

To transition from a legacy, failure-prone commercial logistics system into a deterministic, verifiable, and error-resistant architecture, the introduction of blockchain-backed state anchoring must not only cover the economic logic of transactions but also integrate the communication pathways and physical execution environments — specifically, the warehouse systems, ordering terminals, and client-side interfaces. This section presents a structured model for IP-to-IP communication, event-driven record binding, and transactional anchoring on-chain using BSV as the immutable, cryptographic substrate.

I. Architectural Foundation: Peer-to-Peer (IP-to-IP) Communication and Event Generation

In traditional EDI or ERP systems, inter-party communication is routed through centralised messaging queues, APIs, or polling schedulers. These systems are brittle: state inconsistencies emerge when one party updates records independently or fails to propagate a change to all participants.

In contrast, a peer-to-peer (IP-to-IP) topology enables direct, authenticated transmission of messages — order requests, confirmations, delivery tokens, etc. — between parties, using encrypted channels with time-bounded session keys. This can be secured via ECDH (Elliptic Curve Diffie-Hellman) key exchange, where the public identity of each node is verifiably known, and session-level privacy is enforced.

Each communication event generates:

• A local state change (e.g., order status updated to “pending amendment”)

• A cryptographic transactional anchor: a hash or signature that proves that the message was received, acknowledged, or declined

This event can be recorded on-chain, not as a blob of data via OP_RETURN (which is discouraged), but through hash commitments inside output scripts, structured to trigger conditional UTXOs only when a valid message has been proven by its recipient.

II. Warehouse and Office Logic as Script-Validated Execution Endpoints

Each subsystem (office, warehouse, collection point) can be abstracted as a state agent, with discrete authority to initiate, amend, or confirm transitions. Their authority is modelled through private keys and role-specific script templates.

For example:

• The office system generates an invoice and outputs a UTXO encoding:

  • OP_CHECKSIG of the office’s private key

  • A hash lock to the payment confirmation

  • A redeem condition linked to the expected collection date

• The warehouse node receives an event (via IP message), matches it to the UTXO, and prepares physical release conditional on

  • Valid spend proof of the above output

  • Cryptographic presence of the customer’s authorised preimage or signature

Thus, the state flow is:

1. Order placed → Transaction T₀ created (invoice UTXO generated)

2. Office amends order → New transaction T₁ cancels original via script rejection (via hash condition, timeout, or override UTXO spend)

3. Warehouse verifies the state of T₀ before releasing stock — if T₀’s UTXO is unspent, the order is still valid; otherwise, not

4. Customer arrives → presents signed transaction T₂, spends delivery UTXO, becomes the only authorised collector

III. State Anchoring via Transaction Graphs and Deterministic Timelines

Every stage of this process is independently verifiable through the transaction DAG (Directed Acyclic Graph), where each node (transaction) includes:

• The full logical script of its constraints

• Time-locked conditions where applicable (e.g., nLocktime and the equivalent to CHECKLOCKTIMEVERIFY)

• Multisig enforcement for approvals, if required (e.g., office + warehouse joint authorisation)

Critically, every subsystem does not need to consult a central state. Instead, each party reads the blockchain, checks whether the expected prior condition has been cryptographically satisfied (i.e., a transaction has spent the correct UTXO), and acts accordingly.

No ambiguity exists. Either the correct transaction was mined (i.e., the amended invoice took effect), or it wasn’t. Either the collection token was claimed, or it remains locked. State is not synchronised by instruction—it is synchronised by immutable transition.

IV. Application: Resolving the Double-Pick Problem

In the original failure case:

• Two orders were prepared due to outdated office instructions

• The warehouse had no visibility into which invoice was cancelled

• The customer walked off with both packages

• No cryptographic enforcement existed tying physical fulfilment to invoice payment

With on-chain anchored logic:

• Both the original and amended orders would be pre-encoded as potential UTXO paths

• Only one would become spendable based on time, condition, and signature

• The warehouse terminal checks the UTXO status: if the original is unspent, pick is valid; if it’s spent (by amendment), it is invalid

• The customer can only claim one of the branches — enforced not by policy, but by protocol

Thus, if the invoice is amended and the original UTXO is spent, any attempted pickup using the old reference will fail. Even if the warehouse physically stages both, the validation at the pickup terminal would refuse release of the cancelled package.

V. Communication Layer: Event Propagation via IP-to-IP and Transaction Watching

Between the parties (office → warehouse, warehouse → customer), direct channels using:

• Mutual TLS connections

• Noise Protocol or Libsodium-based authenticated encryption

• Transaction watching over BSV relay infrastructure (e.g., Merchant API, ElectrumX, Teranode)

Each participant is responsible for:

• Listening to changes in transaction status

• Notifying the counterparty of intent to execute (e.g., “I will pick up Order 472-α at Dock 3”)

• Pre-broadcasting their signed transactions for coordination

• Verifying whether the UTXO they plan to spend is still valid (i.e., not cancelled, superseded, or timed-out)

This hybrid model—off-chain coordination with on-chain enforcement—provides an elegant, robust solution. It separates signalling (messaging) from proof (execution).

VI. Final Model: Blockchain as Legal Infrastructure, IP-to-IP as Logistics Fabric

• The blockchain holds the irrefutable truth: what can be done, what has been done

• IP-to-IP communication handles event propagation, scheduling, status notifications

• All commercial enforcement relies on deterministic script evaluation, not paper trails or procedural policies

• Every terminal (ordering system, warehouse kiosk, collection scanner) becomes a validation agent, not a data-entry point

• The entire supply chain, including its error-handling logic, becomes a deterministic machine of proofs

This is not merely process automation. It is the reconstruction of commercial state in a form that cannot be gamed, forgotten, or misaligned. It is truth by design, enacted at the protocol layer, and verifiable by any party at any time. The chain knows no confusion.

Only validity.

Anchoring Supply Chain Execution to Deterministic Blockchain State via IP-Level Coordination and Script-Enforced Transition Logic

By integrating authenticated IP-to-IP messaging with deterministic, script-enforced transitions on-chain, Bitcoin (BSV) transforms supply chain systems into formally verifiable automata, where every physical action—order, amendment, fulfilment, or pickup—is governed by cryptographic proof, not mutable records or procedural trust. Each subsystem (warehouse, office, client) operates as a deterministic state agent, enforcing transitions only when predefined, unforgeable conditions are met. The result is a globally auditable, irreversibly ordered economic state machine, eliminating ambiguity, race conditions, and fraud through provable logic, and ensuring that commercial truth is recorded not as narrative, but as immutable transition.

I. Transition Systems in Commercial Logistics — Automata Foundations

From the perspective of formal systems theory, a supply chain can be modelled as a distributed, multi-agent state transition system, where each event (order creation, amendment, fulfilment, handoff, receipt) represents a discrete state transition. Traditionally, these transitions are neither deterministic nor formally modelled: state is represented via mutable records dispersed across heterogeneously administered systems — ERPs, WMS, POS terminals, logistics APIs — with each agent interpreting the global state indirectly and often inconsistently.

Bitcoin, correctly implemented (BSV), allows for the supply chain to be modelled as a Distributed Deterministic Transition Automaton (DDTA):

• States are encoded as UTXOs — each representing a tokenised commitment of value and/or contractual condition

• Transitions are validated by Bitcoin Script — enforcing precise movement conditions

• Inputs act as deterministic witnesses for state satisfaction

• Outputs define new states, cryptographically bound to constraints

• Edges are mined transactions, forming a DAG of confirmed transitions

In automata theory, this constitutes a finite-state labelled transition system where:

• Σ = Alphabet of economic events (payment, shipment, amendment)

• Q = Set of UTXO configurations

• δ: Q × Σ → Q = Transition function encoded via Script conditions

• q₀ = Genesis state (e.g., uncommitted inventory)

• F = Set of final configurations (e.g., confirmed delivery and reconciliation)

No state transition is valid unless δ(q, σ) can be computed deterministically as q', with all relevant constraints satisfied — not by messaging consensus, but by proof-carrying transaction state.

II. The Dual Ledger Model — Communication Fabric and Execution Layer

Supply chain systems suffer primarily from bifurcation: the message layer (IP-level API signals, form submissions, status updates) and the execution layer (physical fulfilment, delivery, audit) operate asynchronously and are often misaligned. The proposal here introduces a unified, cryptographically-linked dual-layer model:

1. Communication Layer

   • IP-to-IP messaging between actors (order terminals, warehouse systems, courier scanners, customs agents)

   • Events include: order creation, invoice amendment, stock pick request, loading bay assignment, customer pickup notification

   • Channels secured via ephemeral ECDH, authenticated via persistent public identity keys

2. Execution Layer

   • Every critical event is accompanied by an on-chain UTXO transition, validated by Script

   • These transitions enforce the validity of physical execution — e.g., a package cannot be picked unless its UTXO proves authorisation

   • Scripts act as executable guards: they define what must be shown to move to the next state (proof of payment, preimage, digital signature, multi-party unlock)

Each transition corresponds to an edge in a labelled automaton, with the label being both the semantic event and the associated hash-locked constraint. This model reduces execution to functional transition evaluation — no mutable state, no double spend, no replay ambiguity.

III. Script as the Transition Function — Formal Semantics of Control

In a correctly structured logistics chain, each physical transition — e.g., warehouse release, courier pickup, customs clearance — is not triggered by policy, but by the satisfaction of a script.

Formally, Script serves as a validator for δ in the tuple (Q, Σ, δ).

Let:

• s₁ ∈ Q be a UTXO state representing “picked and staged”

• σ be the event “customer presents invoice and signs pickup”

• w be the witness (signature, preimage, timestamp)

• δ(s₁, σ, w) = s₂ is valid ⇔ Script(s₁, w) → TRUE

The script must verify:

• The customer signature matches the committed pubkey

• The pickup occurs within a locked time range

• The preimage matches a hash (e.g., SMS or QR code pre-shared)

• No conflicting UTXO has been spent (i.e., exclusivity is enforced at the protocol level)

If and only if all are satisfied, the transition occurs. Otherwise, the transaction is invalid and not accepted by the network — invalid transitions cannot occur, even if attempted by a dishonest actor.

IV. State Composition and Multi-Stage Paths — DAGs of Supply State

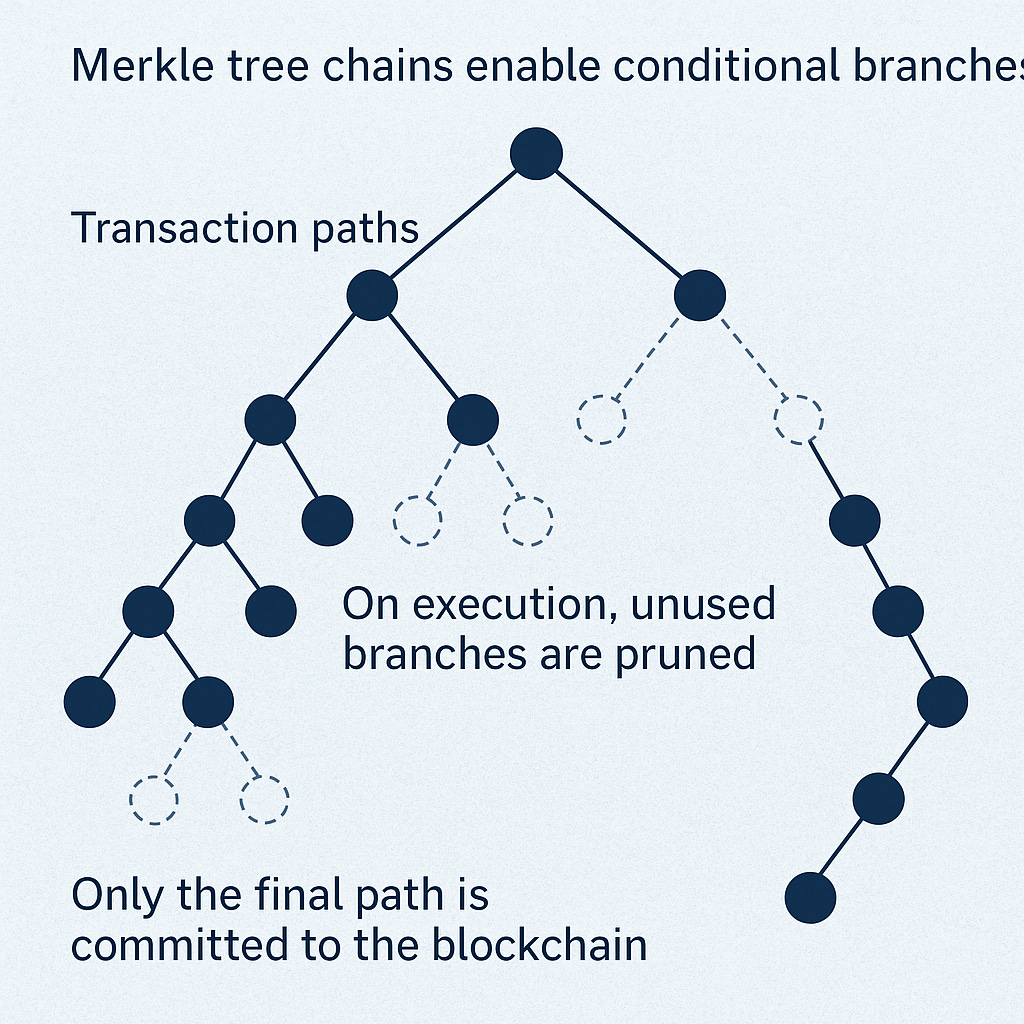
Bitcoin’s UTXO model supports non-linear, branching commercial workflows via multi-output scripts and alternative valid transitions. A supply chain is not a simple linear path — it includes:

• Multi-point distribution (e.g., one shipment → many retail stores)

• Contingency flows (e.g., fallback to supplier if delivery fails)

• Delegation flows (e.g., transfer custody to a new courier)

These are modelled via pre-signed but unbroadcast transaction chains, where:

• Every future state has a valid transaction encoded, but

• Only one path is confirmed through inclusion in the ledger

This mirrors the concept of branching execution trees in nondeterministic automata, except that Bitcoin’s consensus process enforces determinism by selecting a unique path through mining. All possible future paths are structurally known — only one becomes truth.

Each node in the DAG is a transition edge:

• Inputs: cryptographically committed state

• Outputs: new script conditions

• Validity: provable, deterministic, enforced

This allows:

• Warehouse systems to know exactly which state an order is in by watching UTXO spends

• Customs to enforce control by watching time-locked or authority-locked states

• Clients to trust delivery status without API polling — chain state is sufficientV. Terminal Control Points — Linking Physical Access to Script Conditions

At each terminal — warehouse gate, collection kiosk, delivery checkpoint — a thin client (mobile scanner, embedded device, secured tablet) acts as a protocol oracle, not a stateful controller.

Its job:

• Fetch UTXO status via SPV or Simplified UTXO Watch (e.g., ElectrumX or Teranode module)

• Scan customer QR or NFC signature

• Evaluate transaction template with provided witness

• If Script → TRUE, release goods / record pickup / trigger next state

No database lookup is necessary. No state sync is required. The machine enforces a function, not a lookup.

VI. Economic Finality, Not Administrative Reversibility

Legacy systems permit reversals: a shipment can be cancelled via phone call, an invoice voided by database entry, a package rerouted via chat. These are revocable commitments — the source of ambiguity and fraud.

BSV removes this. Every action, once taken and mined, is irreversible. This models commercial truth, not commercial process. Once a customer picks up a package and spends the pickup token, the path is fixed. There is no "undo" — only counter-transitions (e.g., returns, refunds), which themselves must be validated transitions from the new state.

This is not only more secure — it is more legally enforceable. Every actor has proof of their transition, signed and time-anchored. The chain is the audit trail. No argument about who said what. Only provable state changes.

VII. Conclusion: Towards a Formalised, Auditable, Decentralised Commercial Machine

By integrating IP-based authenticated messaging with on-chain transition validation, Bitcoin becomes not just a settlement system, but a universal controller of decentralised state machines for commercial logistics. Every warehouse, every terminal, every customer becomes a node in a synchronised, cryptographically sound transition graph. The state of the world is no longer guessed. It is proven. The flow of goods no longer follows procedural approximations. It follows validated functions. Errors no longer hide in documents. They become provably impossible transitions.

This is not merely EDI on-chain. This is economics as automata, with Bitcoin as the enforcing logic. And it is the foundation for secure, interoperable, and unforgeable supply chain infrastructure for the next century.

Legal and Economic Cost of Intermediated Commerce

Behind the technical failures of EDI lies a deeper cost structure: legal and economic scaffolding constructed to compensate for architectural voids. Because EDI systems cannot enforce execution, they rely on institutional enforcement, contractual ambiguity, and economic externalisation. These dependencies are not incidental. They form the essential economic logic of all EDI-based commerce. Where computation fails to guarantee state, human institutions step in. Where protocols cannot enforce obligations, contracts, courts, insurers, and auditors thrive.

Let us begin with the cost model. In any system where a message cannot be verified, trust must be outsourced. The outsourcing is layered: to internal auditors, external accountants, regulatory frameworks, insurance underwriters, and legal counsel. Each plays a role in resolving disputes that emerge from divergence of belief. The inefficiency is systemic, not incidental. It is inherent to a system that permits syntactically correct yet semantically false statements to pass as commercial actions.

Consider a dispute over non-delivery. Under EDI, a seller transmits an 856 ASN (Advance Shipping Notice), and later an 810 invoice. The buyer remits payment. The goods arrive late or damaged or not at all. The message trail suggests full performance; the physical state contradicts it. The remedy is not computational. It is legal. The buyer must rely on the Uniform Commercial Code (UCC), the Incoterms of the ICC, or other regional legal standards to initiate recourse. This includes documentation, formal notice of breach, and potential litigation. The system does not prevent breach. It presumes it.

Let us formalise the distinction. Let S be the set of syntactically valid EDI message sequences, and let E ⊂ S be the subset that corresponds to fully executed and materially accurate commercial exchanges. There exists no computable function f: S → E such that f(s) = true iff s ∈ E. Instead, f must be evaluated through evidentiary adjudication: document inspection, witness testimony, audit trails, forensic analysis. This is economic deadweight: it adds no productive value, only compensates for protocol insufficiency.

The legal frameworks that support this are structurally conservative. UCC §2-201 (Statute of Frauds) requires contracts for the sale of goods over $500 to be in writing, signed, and sufficiently definite. Yet the standard of “writing” includes electronic messages, which need not be cryptographically signed or deterministically verifiable. As such, the law presumes good faith and allocates burden of proof based on presumptive delivery, customary practice, and transactional history—not formal state machines. These assumptions institutionalise ambiguity.

Insurance fills another role: it monetises failure. In international trade, marine cargo insurance, political risk coverage, and trade credit insurance exist not because shipping is inherently dangerous, but because the commercial record is unverifiable. If delivery and payment were atomically linked—if state transitions were enforced at protocol level—then most categories of trade insurance would become obsolete. Their cost reflects system weakness, not economic necessity.

Auditing is likewise a compensatory mechanism. The audit exists because internal records are mutable and divergent. If transactions were enforced through globally visible, cryptographically bound commitments, there would be no audit gap. Each action would be public, immutable, and irreversibly committed. Yet in the EDI model, audit trails are local artefacts: logs, spreadsheets, XML snapshots. They require external verification, sampling, and reconciliation. This is not validation. It is approximation.

The economic burden is staggering. Estimates from the World Bank and OECD suggest that inefficiencies in trade finance—driven primarily by documentation, reconciliation, and settlement delay—consume 5–10% of global transaction value. In highly intermediated verticals such as commodities, pharmaceuticals, and aerospace, as much as 30% of operational cost stems from dispute resolution, exception handling, and coordination overhead. These are not optional costs. They are direct functions of a protocol incapable of guaranteeing truth.

Let us reframe the question. Suppose instead that each commercial action—purchase order, shipment, receipt, payment—was a state transition on a deterministic ledger. Let σₖ represent the commercial state at time k, and let t be a transaction such that σₖ₊₁ = t(σₖ). If t is valid, the state transition is committed; if not, it is rejected. The conditions are encoded in Script: OP_IF, OP_CHECKSIG, OP_EQUALVERIFY, etc. No external system is needed to adjudicate. There is no ambiguity, no duplicate logs, no audit reconciliation. The action enforces itself.

This model does not eliminate law, but it repositions it. Contracts become constraints encoded in executable logic. Insurance becomes optional, not necessary. Audits become monitoring, not validation. The role of human institutions shifts from interpretation to oversight.

The legacy model thrives on opacity. It creates a secondary economy—lawyers, underwriters, auditors, consultants—whose role is to simulate confidence in a system structurally incapable of enforcing it. Bitcoin collapses that economy by removing the ambiguity that sustains it.

Commerce should not be a matter of trust, remedy, and approximation. It should be a matter of computation, execution, and proof. Until that transformation is complete, legal and economic deadweight will continue to dominate global trade—not because it is necessary, but because the substrate is broken.

Towards Deterministic Commercial State

Commerce is, at root, the transformation of claims into commitments—of promises into provable, irreversible transitions in the allocation of resources. The failure of Electronic Data Interchange (EDI) is not that it fails to carry messages, nor that it cannot simulate workflows, but that it fails to enforce state. Its architecture is fundamentally non-deterministic: multiple actors interpret messages in divergent contexts, each applying mutable logic to partial representations of commercial activity. There is no formal state machine, no canonical source of truth, no global function f such that f(s₀, m₁, m₂, ..., mₙ) = sₙ, where sᵢ are commercial states and mᵢ are protocol-defined transitions. Instead, there are only messages and local interpretations.

The requirement is now inescapable: we must build a system of deterministic commercial state, in which every action is both a declaration and an execution, and every transition is not merely visible, but provable. That is, each commercial event—shipment, receipt, payment—must be encoded as a transaction on a system in which the only possible state change is one that satisfies a set of public, immutable rules. This is not a desire for better infrastructure. It is a demand for computational enforceability.

To formalise this transition, consider the classical model:

• Let 𝔐 be the set of EDI messages.

• Let ℙ be the set of internal programmatic rules within each participant’s system.

• Let Σ be the space of all commercial states.

In EDI, for any message m ∈ 𝔐, the corresponding state update σᵢ₊₁ = P(m, σᵢ) is not globally visible, not reproducible, and not enforceable. Each P is private, mutable, undocumented. There is no consensus engine. No participant can reconstruct the state of trade by inspecting the messages alone, because the interpretation space is undefined and non-commutative.

Now contrast this with the Bitcoin model:

• Transactions are state transitions.

• Each transaction is a tuple t = (σᵢ, σᵢ₊₁, π), where π is a proof: a cryptographic witness that σᵢ₊₁ is a valid successor of σᵢ under the rules of the scripting language.

• The system enforces σᵢ₊₁ = T(σᵢ) only if π ⊨ Script.

This structure is self-validating. No external verification is needed. No manual reconciliation is required. The execution of the transaction proves the action. Nothing more is necessary.

The consequence is revolutionary. In this model:

• Delivery can be enforced as a requirement for payment.

• Receipt can be tied to a signature that enables the release of funds.

• Payment can be conditional, divisible, and redistributable—all encoded within Script.

• Audit becomes trivial: all valid transitions are in the ledger; all invalid attempts are excluded by protocol.

From a distributed systems perspective, this structure yields consistency by design. There is no need for eventual consistency, CRDTs, or reconciliation algorithms. The ledger is the state. From a legal perspective, the transaction is the contract. From an economic perspective, cost is paid only for action—not for verification, litigation, or resolution.

Bitcoin Script—Turing-(in)complete, stateless between invocations, and designed for bounded execution—forces determinism (note a 2PDA is complete over transactions). There are no loops. No dynamic memory. Every path must resolve. This is not a weakness—it is a constraint that ensures that every transaction can be evaluated identically by every participant. There is no ambiguity. No divergence. The result is not a simulation of agreement—it is agreement by construction.

In practical terms, this enables a new architecture for commerce:

1. Each purchase order becomes a script-locked UTXO: a commitment that can only be spent if delivery and confirmation conditions are met.

2. Each invoice becomes a transaction attempt: an execution that only succeeds if the buyer’s policy script is satisfied.

3. Each payment is not a separate act—it is the successful execution of the contract that proves the commercial event occurred.

This architecture does not transmit intention. It enforces action.

The EDI system is a simulation—an expensive, fragile, ambiguous simulation—of commercial truth. Bitcoin, in contrast, is not a simulation. It is a state machine. One in which every step is irreversible, every condition visible, and every transition verified through computation, not adjudication.

The movement from messages to transactions is not merely technical. It is epistemological. It changes what it means to know something occurred in commerce. Under EDI, we believe based on documents. Under Bitcoin, we verify through execution.

In the next section, we will demonstrate how this deterministic structure radically reduces commercial cost—not hypothetically, but mechanically—by eliminating trust, duplication, ambiguity, and dispute. A system that enforces its own state is not an improvement. It is a categorical replacement. It is computation.

Not correspondence.

The Economic Model of On-Chain Truth

The cost of commerce under legacy infrastructure is not the cost of producing goods or transporting them. It is not even the cost of capital or warehousing. It is the cost of verifying truth in an environment where no truth is guaranteed. Every reconciliation cycle, every audit process, every contract dispute, every insurance premium, and every line of compliance software exists because commercial systems do not enforce reality by design. This cost is enormous. It is structural. And it is invisible until made obsolete.

To measure it, consider a standard purchase-to-pay cycle. A purchase order is issued, a shipment is made, an invoice is generated, and a payment is authorised. In a system based on EDI or cloud APIs, each stage requires an independent confirmation. Inventory systems must match shipping records. Invoice terms must be validated against purchase agreements. Payment must be posted and matched. Each of these steps involves human coordination, software integration, error handling, and tolerance for conflict.

Let us formalise this burden. Let C be the total cost of a commercial transaction. Under the traditional model:

 C = cₚ + cₛ + cᵥ + cᵣ + cₐ + cₗ

Where:

• cₚ is the cost of protocol-level messaging (EDI/API transmission fees)

• cₛ is the cost of software integration and maintenance

• cᵥ is the cost of verification (internal controls, matching engines, exception management)

• cᵣ is the cost of reconciliation between systems

• cₐ is the cost of auditing (internal and external)

• cₗ is the cost of legal and dispute resolution processes

Each of these terms is positive because each exists to compensate for the system’s lack of enforceable state. That is, the messaging system cannot itself confirm that a given transaction is real. It requires interpretive effort and trust-based validation at every step.

Now consider the alternative: a system in which every commercial action is an on-chain transaction, enforced through Bitcoin Script, published on a global ledger, and validated by all participants. In this model:

 C' = cₜ + ε

Where:

• cₜ is the transaction fee paid to miners (denominated in satoshis)

• ε is an arbitrarily small operational overhead for local interaction (e.g., transaction construction)

Every other cost—cᵥ, cᵣ, cₐ, cₗ—is eliminated. Reconciliation disappears because there is only one state. Auditing disappears because the ledger is immutable. Verification disappears because script evaluation is deterministic and final. Legal costs drop to zero in all cases where contractual behaviour is governed entirely by script logic.

From an economic perspective, this transformation is radical. The Bitcoin ledger becomes a public enforcement engine, where every transition is backed by proof-of-work, broadcast to all parties, and irreversible once mined. The cost of asserting a fact (e.g., “payment received,” “goods delivered,” “invoice settled”) is the cost of encoding that fact as a transaction and having it accepted into the canonical chain.

This is a world where:

• The truth is publishable.

• The cost of lying is provable rejection.

• The cost of enforcement is zero, because enforcement is computation.

Let us now restate this formally. Let T be the set of all valid transitions, and let L be the ledger. Then:

 If t ∈ T ⇒ t ∈ L
 If t ∉ T ⇒ t ∉ L

That is, the ledger includes only those transitions that satisfy the validation rules—including time locks, digital signatures, hash locks, and policy constraints. This turns commerce into a closed, composable system of state machines. Every step is machine-checked. Every change is visible. Every claim is tested by execution, not interpretation.

The traditional model makes truth expensive. The Bitcoin model makes truth free after publication. The only cost is the act of proving, and that act is paid once per transaction, not per party. The result is a commerce stack where publication replaces reconciliation and execution replaces negotiation.

This is not theoretical. It is happening. Each time a business encodes a conditional payment in a script, or a delivery proof in a hash, or a chain of custody in a Merkle path, it exits the world of human trust and enters the world of computable truth.

Commerce under EDI is bureaucracy. Commerce under Script is logic. The former defers cost by spreading it across departments and delays. The latter collapses cost by absorbing it into code. The economic model of on-chain truth is not just more efficient—it is deflationary by design. It reduces cost not at the margin, but at the root. It does not streamline coordination. It abolishes the need for it.

The only remaining costs are the ones that prove you’re telling the truth. Everything else is discarded, because nothing else is needed.

Summary and Forward Reference

Electronic Data Interchange is not a failure of intent. It is a failure of architecture. It attempts to automate commerce by encoding intention as message formats—yet it cannot enforce that intention, verify its execution, or bind it irreversibly to outcomes. This is not due to technical limitations of past decades, but to a structural flaw: EDI assumes that truth can be reconstructed through communication. It cannot. Truth in commerce must be executed, not merely asserted.

Over the course of this chapter, we have traced this failure across ten interlocking dimensions:

1. EDI’s Historical Origins: Built from punch cards and fixed-width encodings, EDI grew by formalising message layout, not transactional logic. It preserved syntax while deferring semantics.

2. Centralised Control: VANs, API providers, and cloud EDI systems became interpretive authorities—not neutral relays. They inserted opacity and fragility into what should be deterministic processes.

3. API Modernisation Illusion: REST, JSON, and cloud orchestration did not fix this; they accelerated failure by obscuring it with mutable, black-box systems.

4. Decoupled Payments: Value transfer occurs in a different system from messaging, destroying atomicity and enabling fraud, denial, and delay.

5. Epistemic Fragmentation: Every participant maintains a different record of the same event, requiring reconciliation, audit, and dispute management.

6. Message-Level Success, Commercial Failure: Transactions can “succeed” in the EDI system while failing catastrophically in the real world—because message success ≠ event truth.

7. Legal and Institutional Deadweight: Insurance, compliance, dispute resolution, and regulation exist largely to patch a world where software cannot guarantee outcome.

8. Lack of Determinism: There is no global state machine, no transaction ledger, no provable function of state—only logs, interpreted variably.

9. Economic Cost: Billions are spent annually on overhead that exists solely to simulate verification—coordination that becomes unnecessary once computation guarantees execution.

10. Architectural Contradiction: EDI declares intentions through structure, yet relies on humans and institutions to determine whether those declarations were true.

Against this backdrop, Bitcoin emerges not as a payments system, nor as a speculative asset, but as a deterministic, shared-state ledger for encoding commercial truth. Its transaction model, when understood correctly, is not just an innovation in digital value transfer—it is a replacement for the entire class of systems built on interpretive messaging.

In Bitcoin:

• There is no need to reconcile—because every party reads the same state.

• There is no need to audit—because the ledger is cryptographically immutable.

• There is no need to verify post hoc—because validation is performed at execution.

• There is no need to trust—because every claim must be proven before state changes.

Commerce becomes deterministic. Execution replaces intention. Code replaces contracts. Cost is shifted from enforcement to construction: one must build a valid transaction, or nothing happens.

The remainder of this book builds the replacement. We will:

• Construct a full Electronic Data Interchange system over Bitcoin Script.

• Define canonical formats for structured transactional data.

• Encode not just value, but event logic and message flow into spendable outputs.

• Use deterministic scripts to model delivery, receipt, invoicing, settlement, rerouting, partial shipment, refunding, and recomposition.

• Eliminate ambiguity by enforcing facts as executable commitments on-chain.

In the next chapter, we begin with the core substrate: the Bitcoin scripting language itself—not as folklore, not as misunderstood legacy, but as a domain-specific language for conditional state transition, constrained in power but maximally expressive in structure.

Before one can encode commerce as computation, one must understand the machine. Bitcoin is that machine. Script is its logic. Everything else—law, dispute, reconciliation—is what one no longer needs.

Chapter 2: Bitcoin Script as a Deterministic Transactional Machine

Origins of Bitcoin Script: Not a Smart Contract Platform

The idea that Bitcoin Script was ever a limited toy language stems from ignorance—often wilful—of both formal systems and the architecture of Bitcoin itself. Script, in its original design and now fully expressed in BSV, was not created to compete with what marketing departments later dubbed “smart contracts.” It was never meant to simulate the world. It was built to enforce truth. Not by modelling state, but by asserting provable transitions between known, committed states. It is not a VM. It is not a sandbox. It is a mechanical validator of commercial logic, grounded in the formal constraints of a transactional stack machine. It operates with the clarity of predicate logic, not the abstraction of imperative programming.

To understand the origin of Script is to grasp Bitcoin’s architecture as a system of provable conditions, not executable instructions. Every UTXO—unspent transaction output—is not merely a coin or a token. It is a contract. And every contract is governed by its locking script: a predicate which must be fulfilled by the unlocking script of the transaction that spends it. There is no stored state, no variable binding, no mutable memory. There is only the stack and its transformations, and this simplicity is not a weakness but a foundation. Because of it, Script becomes deterministic, analyzable, and cryptographically bound to each specific transition in the ledger.

Bitcoin’s creator didn’t adopt this design accidentally. The scripting system is a minimalist language, heavily inspired by Forth, a concatenative, stack-based language developed in the 1960s for embedded control systems. In Forth, the focus is not on functions but on sequences of operations, executed in reverse Polish notation. This model is not only terse and efficient—it also provides absolute clarity in how data flows through the system. It lends itself to formal analysis and compositional logic. Script inherits this architecture. It doesn't declare variables; it manipulates values directly. It doesn't have functions; it composes opcodes. It doesn't have objects; it has stacks.

This design also owes a conceptual debt to PostScript, the page description language created by Adobe. PostScript, like Forth, represents documents not as imperative sequences of drawing instructions but as declarative stacks of operations on a canvas. Script is no different: it is not drawing pictures, but expressing the conditions under which a transaction may move forward. And like PostScript, the entire computation is represented as a single evaluable expression, whose truth is either accepted or rejected by the machine.

Where mainstream languages aim for general-purpose computation, Script exists to define verifiable transitions. Not simulations. Not stateful applications. Transactions. That is the atomic unit. This is where so many misunderstandings arise: they imagine Bitcoin Script must act like a scripting language inside a process, with variables, memory, control flow, and a runtime environment. But Script is not executed inside a machine—it is executed by the system itself. There is no separate runtime. The protocol is the runtime. There is no sandbox. The script is not a user-defined plug-in: it is the logic of commerce expressed formally and enforced absolutely.

Script was designed to express contractual logic: If these inputs are provided, and these proofs are given, and these hashes match, and these signatures validate, then allow the transaction. It is not about “computing” a result; it is about proving a condition. That distinction matters. Because it is precisely this model that enables distributed consensus without central adjudication. Every node, every miner, every observer who runs a validating client, is not simulating your contract. They are not interpreting your program. They are checking your proof. If the condition is met, the transaction is valid. If not, it is invalid. And that’s the end of it.

Script in BSV restores the original limits and design. It does not strip out opcodes. It does not impose artificial caps. It does not pretend that the system must be neutered in the name of fear. And with these restorations, the full expressive power of Script becomes clear—not in a single transaction, but across transaction chains. When linked in sequence, outputs create state machines. Conditional branches create decision paths. Transactions act as transition functions. You do not need loops when you have infinite extension across transaction space. You do not need state when every state is a UTXO. You do not need memory when every datum is carried forward explicitly. You do not need dynamic behaviour when all behaviour is encoded deterministically.

Script is Turing-complete when used correctly. Not because a single script can loop forever—no script does that, nor should it—but because unbounded computation can be modelled across sequences of verifiable, discrete steps, each defined by the rules of the protocol and enforced cryptographically. This is not hand-waving. This is computability theory. The system is equivalent in power to any model that computes through successive steps and unbounded extension, because transactions can be chained indefinitely. Conditional logic embedded in outputs, consumed only when matched by corresponding inputs, allows for branching, decision-making, and controlled execution over time. This is total computation, expressed over a ledger rather than inside a virtual machine.

Yet none of this makes it a “smart contract” platform. That term is garbage. It was bolted onto a fundamentally different architecture to justify complexity, simulate agency, and lure in speculative capital. But Bitcoin Script does not need to simulate agency. It encodes commitment. It does not pretend to run apps. It expresses binding promises. That is its true role. That is why it works.

This is why commercial systems, EDI, insurance logic, legal conditions, and financial transfers can all be expressed in Script. Not as simulations, not as bloated VMs, but as provable transitions. A delivery that can only be accepted when a timestamp matches. A payment that is released when a hash of an event matches the agreed reference. A transfer that occurs only when signatures from a quorum are presented. A disbursement that splits automatically based on prior allocation. All of these are predicate logic constructs, not imperative commands. And that is what Script provides.

The execution model reinforces this. When a transaction is formed, its inputs reference previous UTXOs. Each UTXO has a locking script. The transaction provides unlocking scripts. The concatenation of these two scripts forms a single expression: the system evaluates that expression on a clean stack. If the final result is a single true value, the input is accepted. If not, the transaction fails. There is no partial success. No side effects. No state leakage. Every computation is atomic and declarative. There is no scope for malleability, no undefined behaviours, no interpretation ambiguity. It either passes or fails. The protocol is the judge, and the proof is the code.

And because the output of one transaction can be the input of the next, entire chains of logic can be constructed. This is how state is modelled: through explicit dependency. Every state is a transaction. Every transition is a spend. Every step is a commitment. This model has more rigour than any imperative language, because it never forgets. There is no garbage collection. No memory loss. No shared state. Just immutable steps.

So why the confusion? Because Bitcoin Core amputated the language. They feared what they did not understand. Rather than restoring the opcodes and exposing the elegance of the system, they lopped off the future. Ethereum, meanwhile, declared that complexity was virtue, that a Turing-complete VM would unlock the world. But they forgot that the purpose of a contract is not to simulate reality. It is to assert terms, verify satisfaction, and enforce outcomes. Bitcoin Script does this natively.

And now, in BSV, it is restored. Every opcode. Every function. Every condition. The system is capable. The scripts are powerful. The ledger is unconstrained. The machine is complete. What remains is the discipline to use it not for spectacle, but for truth.

You do not need gas. You do not need virtual machines. You do not need contract languages that simulate effects. You need predicates. Conditions. Machines that say “yes” or “no” and cannot be bribed. You need verifiable transitions, not emulated events. You need Bitcoin Script.

This is not a smart contract platform. It is something greater. Bitcoin is the truth machine of commerce. And it has returned.

The Stack Model: Execution as Symbolic Reduction

Bitcoin Script, as implemented in BSV, is not a language of commands but of transformations. It operates by symbolic reduction of expressions on a stack, reducing complex conditional logic into a single, final Boolean result. Its structure follows the principles of a LIFO (last-in, first-out) execution model, but unlike trivial examples in pedagogy, this stack is not a toy—it is a symbolic substrate through which logical contracts, financial commitments, and distributed conditions are resolved deterministically. It is not a scripting language in the usual sense. It is not a wrapper around mutable state or heap-driven memory. It is a logical engine, deliberately built to evaluate whether a statement about reality can be accepted as true.

This LIFO stack structure is not just a curiosity of implementation. It imposes strict and precise constraints on composability. Each value pushed on the stack alters the shape of the evaluation context. Each operation consumes and returns values. Unary opcodes transform a single value: negation, absolute value, hash functions, logical NOT. Binary opcodes consume two: equality comparisons, addition, subtraction, multiplications, concatenation. The discipline of stack-based reduction ensures that the structure of every script is self-contained, self-evaluating, and immutably expressed in a single linear segment of code. There are no jumps. There are no loops. There is no external memory or dynamic allocation. All operations are bounded, and therefore, all execution paths are predictable.

This predictability is not a limitation. It is what allows Bitcoin Script to behave as a proof system. A transaction does not carry instructions to be interpreted in a context. It carries a condition to be satisfied. The satisfaction is not dynamic; it is immediate. The concatenation of the unlocking script (scriptSig) and the locking script (scriptPubKey) forms an executable expression. This expression is evaluated deterministically. The script succeeds if, and only if, the stack reduces to a single TRUE value. If it does not, the transaction is invalid. This process of symbolic reduction is absolute. It is not a simulation of execution; it is execution. It does not describe what should happen. It states what is true.

There is no global state. There is no mutable context. There are no frames or stack pointers beyond the evaluation stack itself. There is no recursion. These omissions are intentional. They form the very basis of Bitcoin’s correctness and security. Recursive languages introduce non-termination, ambiguity, and reentrancy risks. Bitcoin Script avoids all of these by refusing to model computation as process. It models it as a finite proof: given these inputs, do these outputs satisfy the declared condition? The entire execution context is captured in the linear script and the stack.

And yet, despite the absence of recursion or state, Bitcoin Script is not computationally limited. It is not a finite state machine in the traditional sense—it is a component of a much larger, global structure that achieves universality through chained transactions and external orchestration. The UTXO model enables total computation by extending execution across the ledger itself. Every UTXO is a snapshot of a system state. Every spend of that UTXO represents a state transition. Every transaction forms a node in a DAG of computational possibility. And each of these nodes is guarded by a Script predicate, defining not what may occur, but what must be proved in order for the system to accept that it did.

The result is a kind of externally navigated, internally strict execution environment—a machine that never lies, because it cannot interpret. In practical terms, the reduction model means that any given script can only succeed when the inputs provided exactly match the constraints of the locking script. A common pattern in this model is the construction of complex logical conditions through nested control structures. A conditional payment may, for instance, include logic such as:

<condition>

OP_IF

<Receiver1_PubKeyHash> OP_EQUALVERIFY OP_CHECKSIG

OP_ELSE

<Receiver2_PubKeyHash> OP_EQUALVERIFY OP_CHECKSIG

OP_ENDIF

This structure performs symbolic branching—not as a runtime decision—but as an enforced logical fork in possibility. Which path is accepted depends entirely on the inputs. The logic is fixed; the options are mutually exclusive; only one can resolve as true. The others remain valid as possibilities, but only one becomes real.

And this brings us to one of the most powerful—and least understood—properties of Bitcoin Script: the externalised modelling of recursion through transaction graphs. While Script itself contains no recursive operations, no CALL or JUMP, and no internal loops, the ledger allows for arbitrarily chained transactions, each depending on the output of the last. This is not merely state—it is computation. Each transaction encodes a logical step. Each UTXO carries forward the computed result. And future transactions may be constructed in advance, ready to be broadcast as soon as the preconditions are met. The entire execution trace of a process can be modelled as a tree of conditional transactions, each one locked by Script, each one representing a possible future.

This tree may include branches that are never executed. Multiple transactions may be prepared to spend the same UTXO. They are valid. They are signed. They are structured. But only one can be accepted. The others are not invalid in logic; they are unrealised. This introduces a level of symbolic expressiveness far beyond typical procedural or VM-bound execution. It models not just what happens, but what could happen, with finality imposed by consensus reality—i.e., the transaction that is ultimately confirmed by miners. This is not double-spending in the malicious sense. It is a model of conditional branching at the ledger level, and it is a key component of Bitcoin's universality.

For example, a warehouse may produce five conditional delivery instructions for the same shipment UTXO. Each path corresponds to a different recipient, delivery time, or payment state. All five are constructed in advance. All five are signed. Only one, ultimately, will satisfy the logical conditions and be confirmed. The others remain as unused logical branches, like skipped branches of a proof tree. They were real. They were valid. But they were not enacted. Script allows this kind of precomputation and conditional logic without central authority. The outcome is dictated by proof—not agreement.

This capacity, when properly formalised, achieves the expressive equivalence of a Turing machine. Not within a single transaction. Not by recursion. But by unbounded construction of conditionally chained transactions, externally ordered and selectively confirmed. In formal terms, it is a distributed, off-chain-evaluable computation with deterministic, cryptographically bounded steps. The Turing completeness arises not from the ability to simulate an arbitrary machine in one script, but from the ability to represent any computational state machine through the ledger's transaction graph, governed entirely by Script-encoded conditions.

The practical result is a model of commerce in which every potential outcome can be pre-defined, signed, and distributed, but only one outcome is enacted. The stack model supports this by ensuring that every transition is pure, total, and irreversible. Once a transaction is accepted, its script cannot be altered. Its outputs are final states. If the system must transition again, it must do so through new scripts, new logic, new proof.

Data structures in this model are not objects or classes. They are positions on the stack. A common pattern is to encode structured information—IDs, timestamps, hashes, pubkeys—as a sequence of pushes, followed by logic that operates on those pushes in a fixed order. There is no parsing. There is no dynamic interpretation. The meaning of each value is defined by its position and its interaction with the opcodes that follow. This creates a kind of typed positional protocol, where structure arises from convention and enforcement, not from syntax.

This model, although rigid, is highly composable. Scripts can be constructed from modular components. A hash check here. A signature verification there. A conditional check. A bounded arithmetic operation. Each component performs one transformation. The stack does the rest. The result is a language of pure logic gates, not instructions. It is closer in spirit to electronic design than to application code. It is a digital logic circuit encoded in symbolic form.

And this is why Bitcoin Script works. Because it cannot be tricked. Because it cannot be reinterpreted. Because its meaning is fixed by its form, and its outcome determined by truth alone. The LIFO model ensures that execution always proceeds in the same way, regardless of context. There is no external frame to manipulate. There is no state to leak. There is only the stack, the code, and the outcome.

This symbolic reduction model—this process of collapsing conditions to TRUE—is what gives Script its power. It is not expressive in the way conventional languages are. It does not allow you to model the world. It allows you to verify that the world has already satisfied a given condition. This difference is not academic. It is philosophical. It is the foundation of all that makes Bitcoin more than a database.

When contracts are written in procedural code, their execution is interpretation. When contracts are written in Script, their execution is verification. Bitcoin does not run code. It enforces conditions. It does not simulate events. It ratifies them. It does not manage state. It requires you to prove it.

Script, as a model of execution, embodies this principle. It is not a script that tells the machine what to do. It is a proposition that the machine either accepts or rejects. And in this acceptance lies the basis of trustless commerce, cryptographic auditability, and total expressive power without ambiguity.

There is no higher form of computation than truth. Script does not ask what should happen. It asks what has already been proved. And by this mechanism, it constructs a universe not of possibilities, but of commitments. A universe built not on mutable simulation, but on immutable decision. That is the power of Bitcoin Script. And that is why the stack is not a convenience—it is the very foundation of symbolic enforcement in a world that finally has a way to make digital truth undeniable.

Script as a Formal System: Deterministic, Composable, Closed

Bitcoin Script, in its restored and fully enabled form on BSV, is not a loose set of operations but a complete, closed formal system. It has a defined syntax, a strict set of evaluable rules, and an execution model that guarantees determinism. It is not a programming language in the modern, open-ended sense. It is a formal system in the mathematical sense—a machine that consumes axioms (stack elements and operations), applies transformation rules (opcodes), and produces truth-valued results (acceptance or rejection of a transaction). Script is not Turing-complete in the local, internalised sense—but it is universally expressive across the transaction space. This composability does not depend on simulation but on formal deductive progression, just as logic systems do.

The fundamental nature of Bitcoin Script aligns most closely with predicate logic, structured through a concatenative symbolic stack. There is no global state. No variable binding. No memory model. What exists is a stream of operations that manipulate a deterministic stack according to strict rules. These rules form the inference system of Script. There is no room for interpretation or variation. Every script is an assertion; every successful spend is a proof. This is not metaphorical—it is the structure of logic itself. Inputs are evidence. Outputs are commitments. The script is the function that links the two.

Formally, Bitcoin Script fits the structure of a closed deductive system:

1. A syntax for expressing propositions (scripts),

2. A domain of evaluation (the stack and opcode rules),

3. A transformation system (evaluation rules for each opcode),

4. A halting condition (reduction to a single TRUE value).

This makes Script not just deterministic, but complete within its domain. Every execution is closed: given a script and a stack, the outcome is always the same. There is no external oracle. No environmental dependency. No conditional path hidden in context. Bitcoin Script is a pure function: it maps an input state (the unlocking script and transaction) to a truth value, based only on internal rules.

This internal consistency allows Bitcoin Script to be modelled as a deterministic finite automaton (DFA). Each script execution is a series of discrete, bounded steps that transform a known state into another. The stack is the current state. Each opcode acts as a transition function. The machine proceeds from one configuration to the next, consuming inputs, transforming the stack, until it either reduces to a terminal state of acceptance or failure. There are no loops. There is no recursion. Each evaluation path is bounded. This structure, while bounded in any single instance, becomes unbounded through transaction chaining, allowing systems to express conditional logic trees, state progressions, and even recursive patterns in aggregate.

Let’s consider this in more technical depth. A DFA is formally defined by a 5-tuple: (Q, Σ, δ, q₀, F), where:

• Q is a finite set of states,

• Σ is a finite set of symbols (input alphabet),

• δ is the transition function,

• q₀ is the initial state,

• F is the set of accepting states.

Script maps directly into this model:

• The stack corresponds to Q, the set of possible configurations.

• The opcodes are the symbols Σ.

• The evaluation rules of Script form the δ function—deterministic transformations of the stack.

• The empty stack with a TRUE result is F, the accepting state.

• The initial input of scriptSig + scriptPubKey defines q₀.

This mapping is not a metaphor. Script executions can be modelled, analysed, and verified using DFA theory. The implications are critical: not only is Script deterministic, it is also predictable and analysable in finite time. Every spend attempt either satisfies the predicate or fails—there is no ambiguity.

This stands in sharp contrast to Turing-complete systems like λ-calculus or modern functional languages, where general recursion, unbounded memory, and side-effects introduce undecidability. Bitcoin Script avoids this by design. It deliberately omits dynamic constructs not because they are unnecessary, but because they are dangerous in a system meant to model truth. Where λ-calculus provides abstraction, Script provides executability. Where general-purpose languages express procedures, Script expresses theorems. It is not a system for simulation, but for verification.

And yet, this does not make Script weak. On the contrary, its expressive precision allows it to model powerful systems—through composition. Rather than creating loops or recursive functions, systems are expressed as chains of transactions, each transaction representing a step in an evaluative process. These transactions can be composed, branched, or conditioned, forming computational graphs that encode complex, stateful processes. The lack of internal recursion is not a constraint on expressiveness; it is an enforcement of discipline. The system is safer, more auditable, and more robust because of it.

Each transaction forms a new axiom. Each UTXO defines a new proposition. Each script enforces a proof that must be satisfied to move forward. This is not a chain of computations. It is a ledger of proofs. It is not a virtual machine; it is a physical system of commitments and conditions, rendered in a form that machines can evaluate but not reinterpret.

The composability of this system arises not from dynamic typing or functional abstraction, but from stack alignment and opcode purity. Each script is constructed from discrete logical parts: a hash check, a signature verification, a condition, a branch. These can be composed into higher-order logic structures using the stack. Just as in formal systems where one proof becomes the basis of another, scripts in Bitcoin can be modular, with each component verifiable on its own, and reusable in broader systems. This makes Bitcoin Script a true compositional logic framework for financial and contractual enforcement.

What emerges from this is a new paradigm for computation—not one built on expressiveness for its own sake, but one built on formal verifiability. Script allows systems to express what must be true, not what should be done. It is a language of commitments, not procedures. It is not declarative in the usual programming sense; it is declarative in the logical sense. It declares that certain conditions, if met, lead to valid state transitions. And the system enforces that these transitions can occur only when the proof is valid.

This is how commerce should work. This is how logic should govern financial systems. Not through dynamically executing code with unpredictable outcomes, but through chains of conditions that can be examined, reasoned about, and enforced without exception. Script is not a tool for simulation. It is a mechanism for proving things about reality. In doing so, it creates a system of truth, not trust—a system of enforcement, not execution.

In summary, Bitcoin Script, as restored in BSV, is a fully formed formal system. It is deterministic, closed, and composable. It can be modelled with DFA theory. It is weaker than Turing-complete systems in isolation, but this weakness is its strength. It prevents non-halting programs. It eliminates ambiguity. It forces systems to be defined in terms of proofs and conditions. When combined with the transaction chaining model, it achieves expressive universality across the ledger, while retaining local certainty in every execution.

It is not a programming language. It is a logic engine.

It is not for simulation. It is for assertion.

It is not for exploration. It is for enforcement.

It is not a model of the world. It is a model of provable truth.

Opcode Taxonomy: The Mathematical Structure of Commands

Bitcoin Script, as restored in BSV, is a strict, minimal formal language composed of symbolic instructions that operate over a stack. Each instruction, or opcode, transforms the symbolic structure of the stack or asserts a constraint about its state. The set of all opcodes forms the grammar of Bitcoin's logic machine. To understand Script not as a sequence of procedural statements but as a grammar is to uncover its true nature: every transaction is a theorem. Every spend is a proof. The system is not open-ended—it is composable, total, and self-contained. And at the heart of this composability is the taxonomy of opcodes.

Each opcode belongs to a mathematically definable class. These classes are not arbitrarily drawn but arise from their arity (unary, binary), logical role (assertion, branching, transformation), and computational class (finite state transition, cryptographic assertion, arithmetic constraint, and symbolic rewrite). In this section, we define these groups formally, outline every opcode in current BSV, and structure them as a logical family tree. The goal is to treat Script as a deterministic formal grammar with a bounded, classifiable opcode set, suitable for automaton-based execution.

I. Core Classifications of Opcodes

Every opcode in Bitcoin Script fits into at least one of the following categories:

1. Stack Manipulation

2. Arithmetic and Bitwise Logic

3. Flow Control

4. Cryptographic Primitives

5. Locking and Signature Verification

6. Equality and Comparison

7. String and Byte Manipulation

8. Constants and Pushdata Operations

9. Reserved and NOPs (ignored by evaluators)

10. Disabled or Historical Opcodes

II. Classification by Function

1. Stack Manipulation (Arity: Unary/Structural)

These operate purely on stack structure, transforming positional values:

• OP_DUP — Duplicate the top item on the stack

• OP_SWAP — Swap the top two items

• OP_OVER — Copy the second item to the top

• OP_PICK — Copy an item n deep to the top

• OP_ROLL — Move the item n deep to the top, removing it from its original position

• OP_ROT — Rotate top three items

• OP_2ROT — Rotate top six items

• OP_2SWAP — Swap top two pairs

• OP_2OVER — Copy pair from position three and four

• OP_DEPTH — Push the current depth of the stack

• OP_DROP — Remove the top item

• OP_2DROP — Remove top two

• OP_NIP — Remove the second item

• OP_TUCK — Copy top item below second item

• OP_IFDUP — Duplicate top item if it is not false

• OP_TOALTSTACK, OP_FROMALTSTACK — Move between main and alternate stacks

• OP_XSWAP, OP_XDROP, OP_XROT — Extended stack operations (BSV extensions)

These instructions define the symbolic environment for script execution. They are non-branching, total functions on stack state.

2. Arithmetic and Bitwise Logic (Arity: Unary, Binary)

All values are interpreted as 32-bit signed integers unless noted.

• OP_1ADD, OP_1SUB — Unary increment/decrement

• OP_NEGATE, OP_ABS, OP_NOT, OP_0NOTEQUAL — Unary transformations

• OP_ADD, OP_SUB, OP_BOOLAND, OP_BOOLOR — Binary logic/arithmetic

• OP_NUMEQUAL, OP_NUMNOTEQUAL — Equality

• OP_LESSTHAN, OP_GREATERTHAN, OP_LESSTHANOREQUAL, OP_GREATERTHANOREQUAL

• OP_MIN, OP_MAX — Comparisons

• OP_WITHIN — Check if x in [min, max)

• OP_MOD, OP_DIV, OP_MUL — Multiplication and modulus (restored in BSV)

• OP_LSHIFT, OP_RSHIFT — Bitwise shifts (BSV-specific)

These opcodes implement the numeric logic gates of Script, allowing the encoding of bounded computational expressions and comparisons. All are total functions on fixed inputs.

3. Flow Control (Branching / Halting)

• OP_IF, OP_NOTIF — Begin conditional branches

• OP_ELSE — Branch separator

• OP_ENDIF — End of branch

• OP_VERIFY — Assert top of stack is true, else fail

• OP_RETURN — Halt execution and mark transaction as provably unspendable

• OP_NOP, OP_NOP1–OP_NOP10 — Reserved for future upgrades (ignored during execution)

These are control operators, not flow operators in the imperative sense. They define evaluative branching only within static execution frames. No dynamic recursion or looping.

4. Cryptographic Primitives

• OP_HASH160 — RIPEMD160(SHA256(x))

• OP_HASH256 — SHA256(SHA256(x))

• OP_SHA1, OP_SHA256 — Direct hash functions

• OP_RIPEMD160 — RIPEMD hashing

• OP_HASHCAT — Concatenate two items, then hash (BSV-specific)

These define digest operations, providing structural binding of transactions and enabling Merkle commitments, origin binding, and hash-locked conditional logic.

5. Signature Verification and Locking Primitives

• OP_CHECKSIG, OP_CHECKSIGVERIFY — Single signature verification

• OP_CHECKMULTISIG, OP_CHECKMULTISIGVERIFY — Multisignature validation

• OP_CHECKDATASIG, OP_CHECKDATASIGVERIFY — Signatures over arbitrary data (BSV)

• nLockTime

• OP_PUBKEYHASH (legacy; implies OP_DUP OP_HASH160...)

These enforce identity, authorisation, and time constraints, forming the heart of all commitment enforcement, escrow, multi-party logic, and delegation.

6. Equality and Boolean Comparison

• OP_EQUAL, OP_EQUALVERIFY — Bytewise equality

• OP_BOOLAND, OP_BOOLOR — Logical conjunction/disjunction

• OP_NOT, OP_0NOTEQUAL — Negation or zero-check

• OP_NUMEQUAL, OP_NUMNOTEQUAL — Numeric equality

• OP_NOP — Logical noop (ignored)

These operate over logical propositions, enabling enforcement of proof satisfaction.

7. String and Byte Manipulation

• OP_CAT — Concatenate two strings

• OP_SPLIT — Split a string at index

• OP_SIZE — Push length of item

• OP_SUBSTR, OP_LEFT, OP_RIGHT — BSV-restored string operators

• OP_NUM2BIN, OP_BIN2NUM — Convert numbers to binary and vice versa

• OP_REVERSEBYTES, OP_REVERSE — Byte order reversals (BSV)

These are essential for structured data encoding, binary protocol enforcement, and complex conditional encoding for multi-party or multi-condition outputs.

8. Constants and Pushdata Operations

• OP_0, OP_1–OP_16 — Constants

• OP_PUSHBYTES_n — Push n bytes (where 0 < n < 75)

• OP_PUSHDATA1, OP_PUSHDATA2, OP_PUSHDATA4 — Push extended data

• OP_1NEGATE — Push -1

These form the literal space of Script—everything else operates on what they place onto the stack.

9. Reserved, Ignored, and Historical Opcodes

• OP_RESERVED, OP_VER, OP_VERIF, OP_VERNOTIF — Reserved for consensus upgrades

• OP_NOP1–OP_NOP10 — Currently ignored, can be repurposed

• OP_RESERVED1, OP_RESERVED2 — Invalid if executed

• OP_CALL, OP_RETURNTRUE, OP_EXEC — Experimental in historical forks (not in BSV)

BSV does not use soft-forkable NOPs for future upgrades. Its philosophy is that protocol rules should be locked and deterministically understood.

III. “Script as Grammar”: Functional Composability Without Variables

The genius of Script is that it behaves like a linear grammar, where composability arises not through function definition or variable abstraction, but through stack position and opcode order. The stack itself becomes the environment. Every value is a token. Every opcode is a transformation rule. What results is a formal language that, when executed, reduces to a verdict on the validity of a transaction.

There is no scope. No mutation. No naming. All structure is positional and symbolic. This means that all Script can be composed without encapsulation, and correctness can be evaluated at compile time. The system is closed under evaluation—there is no execution that leads outside the language.

Alt Stack Manipulation Opcodes

These opcodes manage the alternate stack, a second stack used for temporary value storage. While not frequently used in simple payment scripts, they become essential in complex evaluative structures where temporary values must be saved and later restored without polluting the main evaluation stack. This is particularly important when designing multi-branch conditional logic or nested structural validations.

Primary Alt Stack Instructions

• OP_TOALTSTACK
  Operation: Pops the top item from the main stack and pushes it onto the alt stack.
  Stack before: [..., x]
  Stack after (main): [...]
  Stack after (alt): [..., x]

• OP_FROMALTSTACK
  Operation: Pops the top item from the alt stack and pushes it onto the main stack.
  Stack before (alt): [..., x]
  Stack after (main): [..., x]
  Stack after (alt): [...]

Role and Logical Function

The alt stack commands serve as scratch registers, enabling temporary storage of intermediate computational values. Their utility becomes apparent in:

• Branch comparisons where values must persist across diverging script paths

• Nested control logic, where depth-sensitive stack ordering must be preserved

• Transformation of multi-step hash or arithmetic sequences, especially in templated script reuse

In automaton terms, the alt stack introduces finite auxiliary memory, effectively extending the evaluation model from a pure stack automaton (PDA-like) to a bounded 2-stack model, retaining deterministic reducibility. Since both stacks are bounded and non-recursive, this remains within the finite-state domain but permits higher structural expressiveness without violating Bitcoin’s non-Turing local constraint.

With these included, the opcode model is complete. The alt stack is not optional for compositional script engineering—it is vital for advanced control flow, especially in EDI-like branching, where symbolic values must be stored between evaluative forks without corruption of core stack logic.

IV. Logical Family Tree of Script by Automaton Class

Bitcoin Script, as a formal grammar of symbolic transformation, maps naturally to well-defined automaton classes in the theory of computation. Each family of opcodes aligns with a specific kind of automaton, depending on the transformation's nature, its dependence on state, its acceptance model, and its capacity to encode predicates or transitions. Script, at its most atomic, operates within the deterministic finite automaton (DFA) class—bounded, stateful, and conditionally executable. However, once composition and UTXO chaining are considered, the system, as a whole, behaves as a Turing-complete construct, albeit distributed across transactions and enforced through verifiable predicate logic.

This section presents an exhaustive classification of all Script operations, mapping each family to a corresponding automaton model. This mapping is not merely illustrative. It defines the computational properties of Script and proves that, although each individual script is stateless and loopless, the composition of transactions across ledger space forms a full model of general computation under constraint. The strength of Script lies in its bounded local evaluation and unbounded global expressiveness.

1. Predicate Logic Layer — DFA Core

These opcodes form the foundation of deterministic finite acceptance. They evaluate logical propositions over input values. Each transition in the script is a reduction from condition to result, with a binary verdict (TRUE or failure). These operations map directly to DFA transitions with Boolean acceptance.

Opcodes:

• OP_EQUAL

• OP_EQUALVERIFY

• OP_VERIFY

• OP_0NOTEQUAL

• OP_NOT

• OP_BOOLAND, OP_BOOLOR

• OP_IF, OP_NOTIF, OP_ELSE, OP_ENDIF

• OP_CHECKSIG, OP_CHECKSIGVERIFY

• OP_CHECKMULTISIG, OP_CHECKMULTISIGVERIFY

• OP_CHECKDATASIG, OP_CHECKDATASIGVERIFY

Automaton Class: DFA (Deterministic Finite Automaton)
Acceptance Model: Boolean state acceptance via reduction
Logical Role: Construct and evaluate composite predicates over stack state

Each execution path is deterministic and consumes finite, known input. No loops. No ambiguity. Complete closure in transformation.

2. Arithmetic and Register Automata — Numeric State Evaluation

These opcodes simulate register machine operations. They operate on symbolic integers represented as signed stack elements and return transformations or Boolean outcomes. They model deterministic arithmetic transition functions without side effects.

Opcodes:

• Unary:
  OP_NEGATE, OP_ABS, OP_NOT, OP_0NOTEQUAL, OP_1ADD, OP_1SUB

• Binary:
  OP_ADD, OP_SUB, OP_MUL, OP_DIV, OP_MOD
OP_NUMEQUAL, OP_NUMNOTEQUAL
OP_LESSTHAN, OP_GREATERTHAN, OP_LESSTHANOREQUAL, OP_GREATERTHANOREQUAL
OP_MIN, OP_MAX, OP_WITHIN

Automaton Class: Finite Register Machine
Acceptance Model: Numeric reduction → Boolean constraint or transformed value
Logical Role: Constrain transaction logic based on amounts, indexes, or protocol parameters

Arithmetic constraints provide dynamic conditionality over deterministic execution. Scripts that include these opcodes simulate simple computational predicates that are essential for range validation, threshold enforcement, and structured input checks.

3. Stack Rewriting — Pushdown Automaton Semantics (No Unrolled Recursion)

These operations manipulate stack topology. They define how values are arranged, consumed, duplicated, or reordered. The stack itself behaves as a symbolic tape, with operations equivalent to non-erasing stack transducers. These do not introduce new computational power (since recursion is forbidden), but they make logical composability possible.

Opcodes:

• OP_DUP, OP_DROP, OP_2DROP, OP_OVER, OP_2OVER, OP_SWAP, OP_2SWAP

• OP_ROT, OP_2ROT, OP_NIP, OP_TUCK, OP_IFDUP, OP_DEPTH

• OP_PICK, OP_ROLL

• OP_TOALTSTACK, OP_FROMALTSTACK

• OP_XSWAP, OP_XDROP, OP_XROT, OP_XPICK (BSV extensions)

Automaton Class: Bounded Pushdown Automaton (PDA without recursion)
Acceptance Model: Positional correctness and completeness of symbolic reduction
Logical Role: Structural alignment and conditional storage during evaluation

These operations define the structural shape of computation in Script. Though not recursive, they permit full construction of arbitrarily complex logical expressions, by enabling stack elements to be repositioned and evaluated in stages.

4. Cryptographic Oracles — Stateless, Non-Invertible Transforms

These hash and signature operations act as one-way function gates. They introduce non-algebraic mappings into Script, meaning they cannot be inverted or reasoned about from within the system. Their primary role is to serve as externally provable constraints—conditions bound to identity, content, or randomness—but they are not automaton transitions in the traditional sense. Rather, they are black-box transformations whose results must be externally known or computable.

Opcodes:

• Hashing:
  OP_SHA1, OP_SHA256, OP_HASH160, OP_HASH256, OP_RIPEMD160, OP_HASHCAT

• Signature Binding:
  OP_CHECKSIG, OP_CHECKMULTISIG, OP_CHECKDATASIG

Automaton Class: Oracle-invoking DFA (Non-reversible transition machine)
Acceptance Model: Deterministic transformation based on cryptographic inputs
Logical Role: External truth anchors — binds script logic to cryptographically verifiable real-world claims

These opcodes do not add expressive power in the computability sense, but they anchor Script to external proofs. They enable commitment, authentication, and timestamp enforcement, making Script a binding ledger for events that occurred outside its execution model.

5. Conditional Branching — Finite-State Tree Construction

Branching in Script is strictly evaluative and non-dynamic. OP_IF, OP_NOTIF, OP_ELSE, and OP_ENDIF define strictly bounded control segments. All branches must be statically resolvable and are chosen based on stack truth values. No loops. No recursion. Execution follows one path, and others are ignored.

Opcodes:

• OP_IF, OP_NOTIF, OP_ELSE, OP_ENDIF

• OP_VERIFY (as fail-fast conditional check)

Automaton Class: Deterministic Tree Transducer (Static control automaton)
Acceptance Model: One-of-many conditional path resolution
Logical Role: Binary branching evaluation over predicates

These constructs model non-looping program flow, allowing for mutual exclusion, conditional locking, and state branching within a transaction. When composed across transaction chains, they simulate finite decision machines with externally enforced progression.

6. Cryptographic Constraint Machines — Integrity, Identity, and External Binding

This class includes opcodes which perform one-way cryptographic transformations or verify digital signatures. These are not part of the automaton core—they function as static, deterministic gates that bind internal stack operations to verifiable commitments. Though opaque from the automaton's perspective, these gates enforce absolute truth conditions from outside the system, using hash functions and public-key verification. They are central to constructing systems of provenance, origin authentication, and data anchoring.

Hashing Opcodes (unary):

• OP_SHA1

• OP_SHA256

• OP_HASH160 (equivalent to RIPEMD160(SHA256(x)))

• OP_HASH256 (equivalent to SHA256(SHA256(x)))

• OP_RIPEMD160

• OP_HASHCAT — Concatenate two values, then hash (restored in BSV)

Signature Verification Opcodes:

• OP_CHECKSIG

• OP_CHECKSIGVERIFY

• OP_CHECKMULTISIG

• OP_CHECKMULTISIGVERIFY

• OP_CHECKDATASIG

• OP_CHECKDATASIGVERIFY

Automaton Class: Oracle-bound Deterministic Finite Automaton
Acceptance Model: Transitions conditionally permitted based on externally verifiable cryptographic constraints
Computational Note: These opcodes are non-invertible; they do not extend automaton expressiveness, but bind scripts to unforgeable assertions

These operations do not expand the logic of the stack machine per se—they bind it to real-world facts. A signature either matches a public key over a given message, or it does not. A hash either commits to a value, or it does not. Script does not attempt to interpret these—only to confirm their truth.

7. Structural Determinism — Stack as Finite Tape

The structural operations on the stack itself map most closely to the classical stack automaton model. These are responsible for enabling deeper compositionality of scripts, preserving intermediate values, moving stack elements, and ensuring that complex logical operations can be expressed cleanly without loss of data. These are pure positional transformations, always terminating, always deterministic.

Primary Stack Operations:

• OP_DUP, OP_OVER, OP_2OVER, OP_ROT, OP_2ROT

• OP_SWAP, OP_2SWAP

• OP_PICK, OP_ROLL, OP_NIP, OP_TUCK, OP_IFDUP, OP_DEPTH

• OP_2DROP, OP_DROP

Alt Stack Operations:

• OP_TOALTSTACK

• OP_FROMALTSTACK

BSV Stack Extensions:

• OP_XSWAP, OP_XDROP, OP_XROT, OP_XPICK

Automaton Class: Finite Stack Automaton with Bounded Auxiliary Tape
Acceptance Model: Conformance to structural preconditions for logical execution
Computational Note: These allow scripts to function without variables, purely by stack position and deterministic flow

The alt stack can be treated as an auxiliary register—effectively a second memory buffer, but without allowing arbitrary recursion or indeterminate state. The machine remains deterministic, bounded, and strongly normalising.

8. Byte-Level Transformations — Symbolic Token Machines

These commands allow manipulation of byte sequences, numbers-as-bytes, and literal data. They do not imply meaning in themselves, but enable construction, deconstruction, and transformation of structured symbolic values. Their presence enables encoding of protocols, nested payloads, and interleaved logic within Script. These are the building blocks of data-aware predicates.

Opcodes:

• OP_CAT — Concatenate two strings

• OP_SPLIT — Split byte string at index

• OP_NUM2BIN, OP_BIN2NUM — Convert between number and minimal binary

• OP_SIZE — Push length of top stack item

• OP_REVERSEBYTES, OP_REVERSE — Byte order reversal

• OP_SUBSTR, OP_LEFT, OP_RIGHT — Extract substrings (restored in BSV)

Automaton Class: Symbolic Rewriting System (non-generative)
Acceptance Model: Validity of structural byte composition, for subsequent logical evaluation
Computational Note: Enables structured data validation and execution flow decisions based on subfields or protocol identifiers

With these, Bitcoin Script operates not merely on raw values, but on structured messages. A UTXO can encode an entire logical message flow—interpreted by stack position and verified using these byte-oriented transformations.

9. Constants and Pushdata Opcodes — Lexical Layer

These are not operators but tokens. They form the lexical atoms of the script. Constants establish the basic numeric range; pushdata opcodes govern literal insertion of bytes. Every script is ultimately built from this lexical base.

Constants:

• OP_0, OP_1 through OP_16

• OP_1NEGATE

Pushdata:

• OP_PUSHBYTES_n (0 < n ≤ 75)

• OP_PUSHDATA1, OP_PUSHDATA2, OP_PUSHDATA4

Automaton Class: Literal Generation
Acceptance Model: N/A — These define the domain over which the DFA operates
Computational Note: These are stack constructors—defining the initial state for every computational pathway

All logical transitions in Script are contingent on these values. Without literal inputs, no evaluation path exists.

V. Script as a 2-PDA: Definition, Structure, and Expressive Power

Bitcoin Script, in its original and restored form on BSV, operates as a deterministic symbolic reducer grounded in stack logic. When viewed through the lens of automata theory, the structure of Script execution conforms to a 2-stack deterministic pushdown automaton (2-PDA). While a single-stack PDA has expressive limitations—namely, it is equivalent to context-free grammars and cannot represent full state machines—a 2-PDA is equivalent in power to a Turing machine. It is essential, then, to formalise how Script maps to a 2-PDA and to demonstrate how and why Bitcoin Script achieves full computational expressiveness through this model.

We begin with the structure.

Definition: 2-PDA (Two-Stack Deterministic Pushdown Automaton)

A 2-PDA is a deterministic automaton equipped with two stacks and no other external memory. It is defined formally as a 7-tuple:

M = (Q, Σ, Γ₁, Γ₂, δ, q₀, F)

Where:

• Q is a finite set of states

• Σ is the input alphabet

• Γ₁, Γ₂ are the stack alphabets for the main and auxiliary stacks

• δ is the transition function

• q₀ is the initial state

• F is the set of accepting states

The key to computational universality is that two unbounded stacks are computationally equivalent to a Turing machine. The stacks simulate the tape and control head: one stack for leftward movement, one for rightward. Through symbolic transfer and reordering, any Turing machine computation can be simulated.

Mapping Bitcoin Script to a 2-PDA

Bitcoin Script natively implements this structure:

• Γ₁: the main stack, used for data manipulation, evaluation, arithmetic, comparison, signature checks, etc.

• Γ₂: the alt stack, managed by OP_TOALTSTACK and OP_FROMALTSTACK, serves as a temporary buffer or scratch space, usable for state-like memory and sub-expression preservation.

• δ: the opcode transition system — each opcode defines a transformation of Γ₁ (and optionally Γ₂). There is no ambiguity: each opcode consumes a known number of elements and pushes a deterministically defined result.

• Σ: the script itself — the input alphabet, which includes pushdata bytes, constant opcodes, and execution instructions.

• Q: the implicit evaluation state — although Script is not typically presented as stateful, any branching logic (OP_IF, OP_ELSE, OP_ENDIF) induces control flow states in Q.

• F: a stack with a single TRUE at the end of execution.

Why This Matters: Total Computability without Loops

Traditional critics of Bitcoin Script have wrongly asserted that it is not Turing-complete because it lacks loops, recursion, or jump instructions. But this argument confuses internal state evaluation with global system composition. In reality, Script is compositional: its evaluation model across transaction chains forms a system of computational steps, each of which is proven valid by deterministic script execution.

The alt stack, when used appropriately, enables a two-stack formal system inside a single script. This means:

1. Intermediate computational states can be stored without polluting the main logical sequence.

2. Reordering and preservation of sub-results is trivial, using only OP_TOALTSTACK and OP_FROMALTSTACK.

3. All compound logical structures—multi-branch conditional sequences, deep stack comparisons, signature chains—can be decomposed into pure stack transformations.

Therefore, even without looping constructs, the presence of two independently operable, unbounded stacks, under the direction of a deterministic control system, elevates Bitcoin Script to the same formal class as a Turing machine.

Deterministic 2-PDA vs. Turing Machine: Equivalence

The formal equivalence of a 2-PDA and a Turing machine is proven in automata theory. Every Turing machine can be simulated by a 2-PDA, and vice versa. In the case of Bitcoin Script:

• The main stack simulates movement in one direction.

• The alt stack simulates movement in the reverse.

• Transferring elements between stacks corresponds to shifting the read-write head.

• Each opcode is a rewrite rule; composition of opcodes is a deterministic evaluation path.

• The script body (Σ) is finite, but transactions are composable, making the program potentially infinite in transaction space.

This means that Bitcoin Script’s logical engine, when used across chained transactions with varying conditional branches, is as powerful as any general-purpose computing system, but without the vulnerabilities of unbounded loops or reentrant state.

Practical Consequences: Ledger-as-Tape

The two stacks are local, but the ledger itself becomes the medium of long-range computation:

• A UTXO represents a snapshot of a computational state.

• Spending a UTXO with a script forms a transition to the next state.

• Multiple pre-signed transactions can represent branches in a computational path.

• Only one path will ultimately be confirmed—this is the final acceptance.

Bitcoin Script, therefore, is not just a language—it is a proof machine, constructed over a 2-stack model, where the ledger is the tape, the script is the logic, and miners are the accepting function.

Summary: Script is a 2-PDA in Full

• Bitcoin Script implements a 2-PDA through the main and alt stacks.

• Every script execution is a finite transition; every chained transaction simulates recursion.

• The system, as a whole, is Turing complete in composition, but provably bounded in execution, ensuring termination and verifiability.

• This is not a limit. It is an elevation of computation—built not on speculation, but on truth-enforced transitions.

There are no loops. There is no recursion. But through deterministic evaluation over two symbolic stacks and chained transaction space, Script becomes a total machine—mathematically complete, logically sound, and universally expressive.

Conclusion of Classification

Bitcoin Script, fully restored and unmodified in BSV, is a bounded stack evaluation grammar. It is composed entirely of:

• Pure transformations

• Deterministic evaluation

• External truth binding via cryptographic proof

There is no state leakage, no mutation, and no recursion. And yet, across transaction graphs, it achieves universality—not by simulating a machine, but by executing a truth model. Each opcode, each class, contributes to this architecture. Script is not a programming language—it is a machine logic specification system, and its opcodes are the gates of a formal logic computer made real in ledger space.

That is Bitcoin Script. It is not a clone of anything. It is not a variant. It is original, complete, and sovereign in logic.

VI. Example — Case One: Logistics Chain with Conditional Routing Using 2-PDA Structure and Alt Stack

In this section, we construct a real-world example: a supply chain logistics flow implemented entirely through Bitcoin Script. The goal is to design a complex, verifiable transfer mechanism involving multiple potential delivery destinations, conditional logic, state-preserving operations using the alt stack, and proof-enforced finality. We will demonstrate how the main stack and alt stack (the two components of the 2-PDA model) operate in tandem to encode multiple delivery paths, validate branching logic, and enforce truth over speculative transaction branches.

This example models the handover of a container originating in Shenzhen, passing through customs in Singapore, and ultimately routed to one of several warehouse locations depending on pre-confirmed receiving conditions. The transaction does not use OP_RETURN, includes multiple conditional branches, and makes full use of stack logic.

---

Problem Model: Conditional Transfer of Shipping Container

Actors:

• Origin: Shenzhen dispatch (signs the original UTXO)

• Hub: Singapore customs facility

• Destinations: Warehouse A (Bangkok), Warehouse B (Hanoi), Warehouse C (Kuala Lumpur)

Conditions:

• Only one warehouse may accept the delivery based on a hash-locked confirmation code sent by the warehouse beforehand.

• The delivery must occur within a valid date range.

• If no warehouse accepts within that window, the shipment returns to origin (fallback).

• All logic must be verifiable on-chain, using Bitcoin Script without off-chain oracles.

---

UTXO Locking Script (Output Script of Dispatch Transaction)

We now build the locking script that will only release the shipment to a valid warehouse based on:

1. Confirmation code (a hash-locked preimage)

2. Destination match

3. Signature verification

4. Fallback logic if all others fail

This script uses:

• main stack: live evaluation stack

• alt stack: temporary holding for confirmation hash, destination ID, and fallback control

<confirmation_hash> OP_TOALTSTACK # Store expected confirmation hash

<destination_id> OP_TOALTSTACK # Store allowed destination ID

<fallback_flag> OP_TOALTSTACK # Store fallback control bit

# Step 1: Pull confirmation preimage from unlocking script

<preimage> OP_SHA256

OP_FROMALTSTACK # Retrieve confirmation hash

OP_EQUALVERIFY # Ensure hash matches

# Step 2: Pull destination code from unlocking script

<dest_code> OP_FROMALTSTACK # Pull destination ID from alt

OP_EQUAL

OP_IF

<pubkey_dest> OP_CHECKSIG # If destination matches, verify destination's sig

OP_ELSE

OP_FROMALTSTACK # Pull fallback flag

OP_0NOTEQUAL

OP_IF

<origin_pubkey> OP_CHECKSIG # If fallback allowed, allow origin to reclaim

OP_ELSE

OP_FALSE # Otherwise fail

OP_ENDIF

OP_ENDIF

Unlocking Script for Valid Warehouse Spend

If Warehouse A is receiving:

<preimage> # Known confirmation preimage

<"A"> # Destination code

<1> # Fallback flag = true (unused here)

<sig_A> # Signature of Warehouse A

Unlocking Script for Fallback (No warehouse claims in time):

<preimage>

<"X"> # Invalid dest ID to trigger ELSE

<1> # Fallback flag enabled

<sig_origin> # Signature from original sender

Execution Breakdown (Stack and Alt Stack at Runtime)

At Start:

• Main Stack:
  preimage, dest_code, fallback_flag, signature

• Alt Stack after first three lines:
  confirmation_hash (Γ₂[0]), destination_id (Γ₂[1]), fallback_flag (Γ₂[2])

Execution Step-by-Step:

1. OP_TOALTSTACK x3 — places confirmation_hash, destination_id, fallback_flag into alt stack

2. OP_SHA256 of preimage — produces actual_hash

3. OP_FROMALTSTACK — pulls expected confirmation_hash

4. OP_EQUALVERIFY — fails if preimage doesn’t match

5. OP_FROMALTSTACK — pulls expected destination code

6. OP_EQUAL — pushes 1 (TRUE) or 0 (FALSE)

7. OP_IF:

   • If TRUE → check signature for destination (OP_CHECKSIG)

   • If FALSE → pull fallback flag

     • If fallback is enabled (OP_0NOTEQUAL) → allow reclaim

     • Else → push OP_FALSE → fail

Why This Is a 2-PDA in Operation

This system is not a naive stack machine. It clearly demonstrates:

• Γ₁ (Main Stack): Holds live computation data: the hash preimage, destination code, and signatures. These are consumed and operated on.

• Γ₂ (Alt Stack): Holds persistent control values: the expected hash, the destination identifier, and the fallback flag. These are referenced repeatedly, conditionally evaluated, and restored for execution.

Each stack operates independently but in coordination, exactly as a 2-stack deterministic PDA requires. The script execution is a deterministic function from these stacks to an acceptance condition. It terminates, accepts or fails, and has no side effects or external state.

More importantly: this system can be duplicated for every step in a shipping chain, with each warehouse producing a hash-locked preimage known only to them, signed UTXOs pre-committed but not yet broadcast. Multiple transactions can be prepared, forming a conditional tree of transaction spends. This is externalised recursion. Not through jumps—but through selectively realisable spend paths, governed by Script-enforced conditions.

Resulting Properties

• Immutable Proof of Delivery: Only the intended recipient, in possession of the preimage and signature, can unlock.

• Verifiable Routing Logic: All destination conditions are inside the script and visible to all parties.

• Reclaim Path: Sender can reclaim shipment if nothing happens, and this is verifiably encoded.

• Turing Completeness Through Composition: While no recursion exists in one transaction, the entire logistics process unfolds as a sequence of 2-PDA transitions, forming a total machine of verifiable commerce.

This is not a theoretical model. This is Bitcoin as designed—scripted, conditional, composable, deterministic. And it replaces entire classes of EDI, warehousing, and logistics logic systems with a simple, auditable stack machine that never lies.

Script Evaluation Model: From Inputs to Commitments

Bitcoin Script is not a programming language in the conventional sense. It is not a system for simulation, procedure, or transformation. It is a logic machine. Its purpose is singular: to determine whether a proposed transaction satisfies the conditions of a previous commitment. Script, therefore, does not “run” in the way one runs a program. It evaluates—and its evaluation is strict, final, and binary. Either the transaction is valid, or it is not. Either the proof is accepted, or the claim is rejected. There is no partial success, no fallback execution, no interpretive negotiation. Only deterministic validation of structured logical truth.

This model begins with a fundamental principle: inputs are witnesses, and outputs are commitments.

Inputs as Witnesses, Outputs as Commitments

Every transaction in Bitcoin spends one or more prior outputs—UTXOs (Unspent Transaction Outputs). Each UTXO is guarded by a locking script (scriptPubKey). This script defines the conditions that must be fulfilled in order for the output to be spent. When a transaction attempts to spend such a UTXO, it provides an unlocking script (scriptSig) in the input. This unlocking script contains the evidence—data, signatures, hashes, preimages, or derived conditions—intended to satisfy the locking predicate.

In formal terms:

• Output = a declaration: “This amount may only be spent under condition C.”

• Input = a proof: “Here is the evidence that C is satisfied.”

The locking script is the rule. The unlocking script is the proof submitted for that rule. The evaluation is a mechanical truth-check—Script does not simulate reality; it verifies logical satisfaction.

Concatenation of scriptSig and scriptPubKey → Evaluation

Evaluation occurs by taking the unlocking script (scriptSig) and concatenating it with the locking script (scriptPubKey). This unified sequence is then interpreted left to right by the Script interpreter. The unlocking script runs first, placing data on the stack. The locking script runs second, consuming or transforming that data. The interpreter maintains a single stack, and in BSV, also the alternate stack, through which all execution proceeds. No other state exists. No register, heap, environment, or global memory is used. All logic is positional and structural.

Example:

Suppose an output is locked with:

OP_DUP OP_HASH160 <pubKeyHash> OP_EQUALVERIFY OP_CHECKSIG

And the spending input provides:

<signature> <publicKey>

Then the final evaluated script becomes:

<signature> <publicKey> OP_DUP OP_HASH160 <pubKeyHash>

OP_EQUALVERIFY OP_CHECKSIG

The interpreter pushes <signature> and <publicKey> onto the stack, duplicates <publicKey>, hashes it, compares it to <pubKeyHash>, and, if equal, checks the signature against the original transaction data and the public key.

If every operation succeeds and the stack concludes with a single TRUE, the input is valid, and the spend is accepted. Otherwise, it fails. There is no tolerance for partial correctness or evaluation fallback. This makes Script structurally sound and mathematically closed.

Determinism and Statelessness of Script VM

The Script evaluation environment is deterministic and stateless. Given the same inputs, the outcome is always identical. There is no system context, external environment, or hidden variable that can influence the result. There is no clock, no account state, no contract memory. Only the stack and the script exist.

This determinism is vital. It ensures that miners, validators, auditors, and observers will all reach the same verdict on a transaction. It also ensures that script validation is complete—every execution path is finite, predictable, and analyzable. There is no gas, no infinite loop, no runtime metering. Script avoids Turing traps by eliminating state mutation and recursion. It achieves total computability through composition, not internal memory.

Scripts either reduce to a verifiable truth, or they fail entirely. There is no room for “maybe.”

Temporal Anchoring: Transaction Context Does Not Alter Execution

Script operates in contextual isolation. Its evaluation is completely independent of block height, timestamp, miner identity, or transaction order. There are no context-sensitive opcodes. The protocol does not permit any script to depend on mutable blockchain metadata or environmental variables. This isolation is not incidental—it is foundational. It is what ensures that Script remains a deterministic mechanism for logical evaluation rather than a reactive or stateful system vulnerable to ambiguity or reinterpretation.

The consequence of this is contextual immutability: a script, once written, behaves identically no matter when it is processed. This is what makes transactions portable in time. A transaction can be constructed, signed, and held indefinitely. It can be passed between parties, broadcast a week or a year later, and still behave identically. The logic it expresses is not dependent on timing. It does not degrade. It does not shift meaning. Its validity is based solely on the truth of its internal predicates.

This is essential for the integrity of pre-signed contracts, multi-branch execution paths, and compositional systems. Without immutability of script behaviour, conditional transactions prepared in advance would risk being invalidated by changes in context. Warehousing logistics, payment splits, escrow triggers—all would become fragile, unpredictable, and unsafe.

But because Bitcoin Script is strictly deterministic and temporally agnostic, it supports pre-signing, offline construction, reusable commitments, and decentralised orchestration of complex logic trees. A party can construct multiple valid spend paths without any of them becoming ambiguous over time.

The ledger does not execute code—it validates conditions. And temporal anchoring happens outside the script. It is expressed not in the logic itself, but in the commitment of transactions to the blockchain. Execution order is enforced through mining, not by internal timing logic. This division preserves the purity of Script and ensures that logical truth is never contingent on mutable context. The machine proves; it does not guess. The chain orders; the script enforces. This only works because script immutability is absolute.

Deferred Execution and Off-Chain Contract Viability

Because Bitcoin Script executes in isolation from block context and external state, it enables the creation and holding of contracts that are entirely off-chain, fully formed, valid, and unexecuted, for indefinite periods. These contracts are not speculative code or abstract conditions—they are real, signed transactions that can be held in cold storage, passed between parties, or escrowed by design. Their validity is not affected by protocol updates, software version changes, or the progression of time. What is locked in Script remains locked exactly as written—bitwise identical, semantically identical, and logically inviolable.

This allows complex agreements to be established long before their execution. A logistics firm can pre-sign all possible shipment paths for a five-year distribution agreement, with each path encoded in Script. Each signed transaction enforces its own conditions: delivery proofs, hash commitments, multisignature requirements, or destination restrictions. As real-world conditions evolve—such as a warehouse confirming receipt or a jurisdiction authorising customs release—the correct branch can be selected and broadcast, while all others remain inert.

No central scheduler is required. No event listener or daemon process is needed to “watch” or interpret blockchain state. The truth of the contract is self-contained, and the act of confirmation—via mining—is the final trigger. This model is impossible under stateful systems or virtual machines. In those, timing, gas availability, storage rent, or external contract state introduce decay, unpredictability, and eventual failure. In Bitcoin Script, the contract remains valid until its inputs are consumed. If no input is spent, the contract is eternal.

This opens possibilities that no other system affords: multi-party deals that outlive the parties, conditional gifts passed across generations, financial instruments that mature on evidence alone, and entire supply networks pre-scripted without execution risk. Bitcoin Script makes the logic of future action decidable in the present—and enforceable at any point where proof is available. It is not a contract engine—it is a time-insensitive machine for unchanging logic, where the truth of execution waits patiently until called.

Enforcement of Spending Conditions as Verification of Input Truth

The complete system becomes:

1. A locking script commits to a condition—a proposition about what must be true for a spend to occur.

2. The unlocking script provides a proof—a sequence of stack manipulations and data elements that must reduce to TRUE.

3. The combined script is evaluated by every full node independently.

4. If and only if the evaluation ends in TRUE, the input is valid.

5. If all inputs of the transaction are valid, the transaction is included in the chain.

There is no room for discretion. No possibility of conflicting interpretation. Every script is a closed logical structure, and every spend is a claim against a previously declared contract. The script is not flexible. It is strict. Not dynamic. Deterministic.

This evaluation model turns Bitcoin into a global proof engine. Each transaction is a theorem, submitted for verification. Each output is a hypothesis. Each input is a claim that the hypothesis is satisfied. Script enforces that claim. The miners confirm it by incorporating it into the chain.

This is the structure of truth—not computation for its own sake, but evaluation of commitment. Bitcoin Script is not a language of possibility. It is a language of proof. And in this, it is not just computational—it is logical, auditable, and final.

Enforcement of Spending Conditions as Verification of Input Truth

The complete system becomes:

1. A locking script commits to a condition—a proposition about what must be true for a spend to occur.

2. The unlocking script provides a proof—a sequence of stack manipulations and data elements that must reduce to TRUE.

3. The combined script is evaluated by every full node independently.

4. If and only if the evaluation ends in TRUE, the input is valid.

5. If all inputs of the transaction are valid, the transaction is included in the chain.

There is no room for discretion. No possibility of conflicting interpretation. Every script is a closed logical structure, and every spend is a claim against a previously declared contract. The script is not flexible. It is strict. Not dynamic. Deterministic.

This evaluation model turns Bitcoin into a global proof engine. Each transaction is a theorem, submitted for verification. Each output is a hypothesis. Each input is a claim that the hypothesis is satisfied. Script enforces that claim. The miners confirm it by incorporating it into the chain.

This is the structure of truth—not computation for its own sake, but evaluation of commitment. Bitcoin Script is not a language of possibility. It is a language of proof. And in this, it is not just computational—it is logical, auditable, and final.

Why Script Isn’t (Traditionally) Turing Complete in a Single Transaction (Other Than as a 2PDA) — and Why That’s a Feature

Bitcoin Script, in its native, unmutated form as restored in BSV, is not Turing complete within a single transaction. This is not a flaw. It is not an omission. It is not a restriction imposed by ignorance or conservatism. It is a deliberate architectural design, constructed to ensure that every piece of logic expressed in the system is finite, decidable, and fully verifiable by every participant, on every machine, at every point in time. It is not a machine for simulation—it is a machine for truth enforcement.

To begin with, Script contains no general looping construct. There is no OP_JUMP, no OP_LOOP, no label or branch instruction capable of introducing unbounded iteration. There is no instruction to repeat execution, no re-entry mechanism, no dynamically determined flow control. Script flows linearly, deterministically, and to completion. Every opcode executes once and only once. Every evaluation path is statically bound by the length of the script and the rules of the stack. There are no side channels, no fallbacks, no deferred branches. The machine is strictly terminating.

The consequence of this structure is that Script execution always halts. This is not merely a convenience—it is a logical imperative. The halting problem, which defines the undecidability of program termination in Turing complete systems, does not apply here. Bitcoin Script can be verified in bounded time by all nodes. This is critical for consensus: miners must evaluate whether a transaction is valid, and they must do so deterministically, without subjective judgement or open-ended computation. This property guarantees universal verifiability, a non-negotiable prerequisite for a distributed financial ledger.

The absence of unbounded computation makes Script unsuitable for arbitrary logic. You cannot use it to compute Fibonacci sequences, simulate physics, or run neural networks. But Bitcoin was never designed to do these things. It was built to enforce contracts, not to model systems. It is not a computing environment—it is a proof system for financial commitment. The value of Bitcoin lies not in expressiveness, but in verifiability. In Bitcoin, correctness outweighs creativity. Precision exceeds generality. Truth is more important than potential.

What Script does permit is bounded computation, finite conditionality, and compositional logic. As shown in prior sections, Script is structurally equivalent to a 2-stack pushdown automaton. And this matters: the moment you extend a PDA with a second stack, it becomes computationally equivalent to a Turing machine. This is not speculative—this is established theory. A 2-PDA, even without loops or unbounded recursion in a single frame, can compute any partial recursive function when allowed to compose state across time.

This composition occurs not within a single transaction, but across the transaction graph. A transaction represents a node. Its inputs define a known state. Its outputs define the result of a computation. The satisfaction of its script enforces the validity of that transition. And because transactions can be chained indefinitely, each enforcing a bounded step of logic, the graph itself forms a tape of deferred computation. The ledger becomes the memory. The transaction order becomes the control. The sequence of evaluations across time becomes the machine.

Thus, while Script itself is not Turing complete in the moment, Bitcoin as a system is Turing complete in composition. This is the key distinction. Computation is not forbidden—it is simply externalised. Each computational step is pre-validated, pre-signed, and bounded. The system does not simulate programs—it evaluates proofs. Every spend is a theorem. Every validation is a derivation. The machine is not inside a transaction. It is the chain.

This structure has profound commercial implications. It means that Bitcoin can enforce contracts with absolute certainty. It means that anyone can verify the correctness of a transaction without guessing, interpreting, or simulating. It means that multi-step workflows, supply chains, escrow agreements, deferred options, and distributed conditional transfers can all be modelled with perfect determinism, without the risk of execution failure, gas exhaustion, or reentrancy.

Other systems invite generality and drown in ambiguity. Bitcoin invites precision and achieves immutability. Script's non-Turing nature in the local frame is not a limitation. It is the foundation of global computational truth, bounded in the small, total in the large, and permanent in its enforcement.

Determinism Without Restriction: Pruning Paths and the Nature of Forward-Only Computation

Bitcoin Script, precisely because it is not Turing complete in a single transaction, achieves something far more powerful in a distributed, compositional system: unbounded future computation with immutable historical anchoring. In practical terms, this means that while Script cannot simulate arbitrary loops or recursion inside a transaction, it enables unconstrained conditional logic across transaction space. This is the model of time in computation: forward-only execution, with branching possibilities encoded in advance, and decisions enforced irreversibly by inclusion in the ledger.

This system is not abstract. It is concrete, physical, and reflects the structure of real-world logic. In life, we are always surrounded by possible futures. At any moment, we can choose to act in one of many ways. We can prepare multiple outcomes. We can sign agreements, issue options, schedule future transfers. But once a path is chosen and executed—once a decision is enacted—it becomes final. We cannot reselect paths. We cannot unact. The rest of the tree falls away. Bitcoin, when used properly, captures this model with mathematical clarity.

A user can construct a billion possible transactions, each representing a possible future. Each one is real: it is signed, structured, and fully valid. These transactions can be chained, forming trees, DAGs, or layered conditional flows. Each transaction represents a single, atomic state transition. Together, they represent a multi-dimensional possibility space, where the next move depends on an externally verifiable condition—hash, signature, preimage, delivery, payment, timestamp, quorum.

What’s critical is this: these transactions can be constructed off-chain. They can be built, signed, and distributed without needing to be broadcast. They represent latent branches in the computation, each of which may or may not be realised. Preconditions are evaluated off-chain, just as we evaluate facts in life: did the customer confirm receipt? Did the warehouse provide a matching key? Did a payment arrive from a counterparty?

Once a precondition is satisfied, the corresponding transaction is broadcast. It becomes part of the chain. That branch is realised, and the others are discarded—not because they were invalid, but because they were never enacted. The past is fixed. The ledger prunes the tree. Only the path chosen remains. This is not just computational integrity—it is time integrity.

Importantly, this structure allows for layered computation. Each chosen path may itself contain further unchosen branches. These may also be prepared in advance: transactions nested into transactions, each conditional on yet-unsatisfied predicates. The system thus permits nested option trees, future-locked decision graphs, and deep, recursive planning structures without requiring any transaction to contain general-purpose looping or recursion. It is external recursion, imposed by transaction topology and enforced by cryptographic truth.

And the system guarantees that no matter how deep the chain, how broad the tree, or how complex the logic, only one path is ever enacted. That path is verifiable, non-reversible, and unique. Once a UTXO is spent, it is gone. Its conditional logic is no longer relevant. The decisions encoded in its descendents, no matter how deeply nested or carefully constructed, are no longer accessible unless they are part of the realised path.

This turns Bitcoin into a model of forward-only computation, where every future possibility can be pre-signed and validated, but only the realised reality enters the global state. It mirrors the structure of a contract: a set of conditional clauses, any one of which may become binding. But only the clause that is enacted by facts becomes enforceable. The rest remain hypothetical.

This approach offers not only determinism and verifiability, but also scalability of logic. Complex automated systems—logistics, escrow, trade flows, multi-party contracts, time-delayed delivery paths—can all be structured through transaction graphs. Script is the validator. Signatures are the enablers. Miners are the ratifiers. And the chain is the history—not of computation, but of decision.

The absence of OP_LOOP or OP_JUMP ensures that each step is auditable. But the presence of unbounded, conditionally-linked scripts ensures that each system is computationally total. Bitcoin achieves Turing completeness not by simulating a machine in memory, but by projecting computation into space and time, anchoring decisions into an irreversible timeline, and proving truth through finality. This is not a bug. This is how reality works. Bitcoin, when correctly understood, is not just a monetary protocol. It is a deterministic machine of deferred truth. And Script is its logic gate.

The Role of OP_RETURN — Metadata Without Execution

In the design of Bitcoin Script, OP_RETURN occupies a peculiar, highly delimited niche—a kind of executional cul-de-sac, an endpoint marker beyond which no computational semantics apply. It is not merely a signalling opcode; it is a deliberate construct for disallowing execution. It aborts evaluation. It ends consideration. And it does so by burning the output, transforming what would otherwise be a spendable UTXO into inert metadata, forever unspendable and programmatically ignored. This mechanism was introduced to preserve the conceptual clarity of what a transaction output represents: not a container for arbitrary data, but a contractual offer—a promise of redemption under precisely specified conditions.

To invoke OP_RETURN is to withdraw that offer.

An output that begins with OP_RETURN is treated by all honest nodes as provably unspendable. There is no locking condition to be satisfied. There is no evaluation path. In formal terms, the inclusion of this opcode causes the validation machine to immediately halt, marking the script as satisfied trivially and terminally false in terms of spendability. In other words, it provides a deliberate path to irrelevance—not for the transaction as a whole, but for that specific output.

This is not a bug. It is a control. A scalar gate on expressivity.

Bitcoin’s ledger is not a sandbox. It is not a global state machine in the Ethereum sense, and it is not a memory store for ad-hoc data fragments. It is a proof ledger, where every spendable output carries a semantic payload: “This can be redeemed if and only if these conditions are met.” That is the logic of Script. To mark an output with OP_RETURN is to excise it from that logic—to say, in essence, “This output exists for visibility, not for value.” It cannot be used in further computation, cannot be referenced as an input, and thus has no bearing on the evolution of Bitcoin’s state.

And yet, in practice, OP_RETURN has been frequently misunderstood—and worse, misused—particularly by those coming from paradigms infected by the procedural and state-oriented views of Ethereum and modern BTC token-layer models. In these systems, control flows, balances, ownership hierarchies, and execution logic are often mapped to arbitrary blobs of JSON, base64, or hexadecimal data appended to the ledger through OP_RETURN fields or analogues.

These approaches are deeply flawed. They conflate visibility with verifiability, and data presence with logical binding. A contract is not proven by its inclusion in an OP_RETURN field. A token balance is not enforced by a string of hexadecimal text lodged in a ledger entry. These are side-channel semantics, dependent on off-chain indexing, custom node software, and unverifiable execution models that run outside of Script. In effect, such uses transform Bitcoin from a proof engine into a write-once memory tape—visible, yes, but uncomputable, unenforceable, and easily corrupted.

BSV—the implementation of Bitcoin as defined in the original whitepaper and preserved with protocol integrity—rejects this mutation. In BSV, Script is not an optional validator. It is the primary and only execution context. It determines truth. It determines ownership. It determines control. And within that model, OP_RETURN is treated with extreme caution. It is not a general-purpose data insertion tool. It is a tombstone.

The role of OP_RETURN in BSV is thus reoriented toward limited metadata signalling, and only in contexts where no control, no transfer, and no redemption is necessary or intended. Examples might include anchoring external state by including a hash of a document, or denoting the creation of an on-chain envelope for notarisation or reference purposes. Even then, Script-based alternatives exist, such as using multisig outputs where one key is never revealed, or hashing data into redeem scripts directly—methods that preserve executional semantics while enabling verification.

What is crucial to understand is that OP_RETURN is never used to define control logic. It is not a conditional gate. It is not a state oracle. It is not an ownership marker. These uses are fundamentally incompatible with Bitcoin’s design. They violate the premise that every UTXO must be programmatically validatable by all honest nodes—without reference to external state, databases, or indexing layers. Script is closed, stateless, and deterministic. Anything placed outside of it—especially in OP_RETURN—falls outside of consensus.

To formalise this distinction:

• Spendable outputs: Constructed with Script logic. Require satisfaction of predicates. Can reference signatures, public keys, hashes, and be composed into combinatorial systems.

• Unspendable outputs (OP_RETURN): Carry data only. No logical conditions. Cannot be redeemed. Serve as inert markers, and are ignored by validation logic.

When used correctly, OP_RETURN becomes a clean semantic separator—a declaration: “This output is not a contract. It is not part of the value system. It cannot be spent. It is not executable.” It is the non-value assertion, the NAND of transactional meaning.

In the context of building a global Electronic Data Interchange (EDI) infrastructure on BSV, this has profound implications. Contracts, tokens, flows, conditionals, delivery confirmations, multi-hop authorisations—none of these should ever be built on OP_RETURN. They belong in Script. They should be validated, not indexed. They should be composable, not scraped. And above all, they should be part of the proof—not part of the commentary.

When BSV re-established the unbounded script capability and removed arbitrary limits on stack size, script length, and data elements, it reclaimed this vision: Script as the machine of verification, not just a gatekeeper of hashes and keys, but a full-fledged logic engine for contractual automation. Within this machine, OP_RETURN is not a shortcut. It is a side exit. Use it with caution, or not at all. Because Bitcoin doesn’t run on commentary. It runs on truth. Script is where that truth is enacted. Let it speak for itself.

Caveat: Misuse Does Not Imply Validity

The existence of OP_RETURN as a mechanism to insert metadata into the blockchain does not imply that it should be used to emulate state, control, or ownership. Its presence is not an endorsement of off-chain state systems, token layers, or the embedding of logicless assertions into irreversible public ledgers. Capability does not entail legitimacy.

What many systems have done—especially those following BTC-style and Ethereum-inspired models—is treat OP_RETURN as a generic data append mechanism, inserting token balances, smart contract pseudo-logic, or identity payloads in the form of text blobs, JSON, and indexed state fragments. These constructions may be visible, but they are not verifiable. They rely not on Script, but on external, unverifiable, centralised logic that must interpret the content—often without consensus, often differently across implementations, and always outside of the native Bitcoin machine.

This is not valid use in the model of Bitcoin as described in the whitepaper and as re-established in BSV. Bitcoin is a machine of proof, not of speculation. It proves who can spend what, under which deterministic, pre-agreed conditions. It does not interpret arbitrary strings in unspendable outputs. It does not infer meaning from commentary.

Therefore, the fact that OP_RETURN can be used to carry arbitrary data is irrelevant to its proper role in the protocol. It is a burn marker, not a computational hook. Its use should be strictly limited to non-control metadata, where inclusion aids human interpretation but does not affect execution, control, or the enforcement of contractual conditions.

In sum: just because others have abused OP_RETURN does not mean such usage is valid. Visibility ≠ validity. Presence ≠ proof. Script alone defines the rules of control. Anything else is commentary. And Bitcoin does not execute commentary.

Script as a Transition System — DFA, Not VM

I. Script as Deterministic Finite Automaton

Bitcoin Script is not a virtual machine in the Turing-complete sense. It is not a computational sandbox with general-purpose memory and arbitrary branching. Instead, it is best understood as a Deterministic Finite Automaton (DFA), where the set of stack states, the list of opcodes, and the evaluation pathway form a bounded, verifiable transition system. Every opcode in Bitcoin acts as a transition function. Each script execution is the reduction of a state stack from a known configuration to a final acceptance state or failure.

The DFA model begins with an initial state: the execution stack at the start of script evaluation (typically empty or populated from scriptSig). As the script is executed, each opcode deterministically transforms the current stack configuration into another. There are no nondeterministic transitions, no ambiguous branches, and no undefined states. Every path is well-defined, and the system must always transition to a terminal result: acceptance (TRUE) or rejection (FALSE).

There are no OP_JUMP or OP_LOOP opcodes. Each script is parsed linearly. Flow control, if present (OP_IF, OP_ELSE, OP_ENDIF), is statically determined by preceding stack values and resolved without recursion. This makes each execution path finite, predictable, and traceable — key properties for auditing financial transactions.

II. Stack Configurations as Automaton States

In this DFA representation, the state is the exact configuration of the stack at any given moment in execution. This includes the main stack, and where relevant, the alternative stack (alt stack), both of which are bounded in size and operation. At each step, the automaton moves from one stack configuration to another based on the application of an opcode.

For example, applying OP_ADD to a stack [3, 5] results in a new stack [8]. This is a single state transition from state s₀ = [3,5] to state s₁ = [8]. Every opcode is a pure function from one valid state to another, with failure resulting in halting and invalidation.

Because the system has no side effects, and because all inputs are known in advance (no hidden state, no memory, no external oracle), it is possible to represent any script as a fully unrolled transition graph. This makes formal verification tractable: one can reason about all possible state transitions statically, ensuring correctness before execution.

III. Script as Stateless Transformer: No Side Effects

The Script engine has no global memory, no heap, no registers, no I/O ports, no open files, no inter-thread communication, and no entropy. Its only “state” is the stack, which lives and dies within the scope of a single transaction input evaluation.

Because of this, Script acts purely as a stateless reducer — a transition system with no memory of the past and no capacity to influence the future except through transaction outputs. This makes it fundamentally different from a virtual machine like Ethereum’s EVM, which maintains a global shared state, a storage trie, a gas counter, and runtime I/O semantics.

This lack of side effects eliminates entire classes of security flaws. There can be no data races, because there’s no concurrency. There can be no memory corruption, because there’s no memory to corrupt. Every transformation is local, atomic, and internally consistent.

This purity of operation is not a weakness; it is a design for resilience. Bitcoin doesn’t pretend to model reality — it simply encodes logical conditions that must be fulfilled for a transaction to be accepted. The transaction is the message. The Script is the proof.

IV. Terminal Transitions: Every Spend Ends the Automaton

A Bitcoin UTXO (unspent transaction output) is a closed statement — a claim made by a prior transaction, locked with a script that defines how it can be spent. When a transaction input attempts to spend it, it must supply data (scriptSig) that satisfies the constraints of the locking script (scriptPubKey).

The concatenated scripts (scriptSig followed by scriptPubKey) form a complete automaton, where the unlocking portion provides data and the locking portion provides validation. Evaluation of this combined script always ends in a terminal state: either TRUE (valid spend) or FALSE (invalid spend). There is no continuation. There is no partial acceptance. The automaton halts — and based on its terminal state, the transaction is either included in the block or rejected.

This finality is essential. Bitcoin does not allow side effects between incomplete script runs. A spend either happens in full, or not at all. This property guarantees that all nodes arrive at the same consensus result using only local deterministic rules.

V. No State → State Propagation via Transaction Graph

Because scripts are stateless, state in Bitcoin must be modelled through chains of transactions. Every change to system state — ownership, value, commitments, data — is expressed through new UTXOs, which become the only inputs to future transitions. This is fundamentally message-passing, not memory mutation.

If one wishes to implement a multi-stage contract, each stage must be a new transaction, spending the output of the previous. Each transaction must define a new set of conditions for the next step. This mimics the behaviour of a state machine built across a directed acyclic graph (DAG) of transactions.

Such transaction chains can model arbitrarily complex workflows: multi-signature escrow, dispute resolution, supply chain audits, and more. They do not require Script to be mutable — instead, they encode future branches of execution, with each step pre-defined, signed, and optionally held off-chain until needed.

This is Bitcoin’s answer to dynamic state: state is not stored — it is passed. The history of changes is not an ephemeral memory log but a permanent, immutable record of actions taken and verified. The ledger is the memory, and it never forgets.

VI. Message-Passing Formalism and Canonical Composition

In this message-passing model, scripts can be composed functionally. A transaction can be seen as a function, where inputs are arguments, the script is the body, and the outputs are the return values. Composing transactions becomes function composition: the output of one function becomes the input of the next.

This aligns perfectly with canonical models in automata theory. The transaction graph is a chain of DFAs, each independently verified, each consuming the final state of the previous as its initial state. As with logic gates, the output is a fixed function of the input. No execution state is retained. No simulation is needed. Bitcoin thus becomes a distributed composition engine, with each transaction acting as a verifiable transition in a globally auditable process.

This model supports parallel execution. It supports pre-signing. It supports delegation. It supports conditionally activated execution branches. And yet it never violates determinism, because every transaction can be independently verified with no reference to global state.

VII. Practical Implications: Contracts as Deferred Machines

Because state is passed in the form of transactions, and execution is stateless, Bitcoin allows a unique form of contract execution: deferred activation. One can pre-define a tree of possible future outcomes — each encoded as a transaction — and selectively broadcast only the valid branch once conditions are known.

This is deeply aligned with real-world commercial logic. Contracts do not execute all branches at once. They define conditional paths: If party A performs X by date D, then funds release; else refund to party B. Bitcoin allows these conditional paths to be represented in advance, verifiably, cryptographically signed, and unforgeably encoded.

No other system allows this model to be deployed at scale without introducing state pollution, storage bloat, or oracle reliance. Bitcoin’s DFA model ensures that every script is isolated, pure, and provably terminating. And because it is stateless, the entire logic tree can be distributed, reviewed, validated, and stored offline, awaiting only selective activation.

VIII. Theoretical Context: DFA ≠ Limited System

Some misinterpret the term DFA as indicating simplicity or constraint. But the truth is that DFAs are the building blocks of computation, not the rejection of it. When composed through transaction chaining, Bitcoin’s stateless DFAs achieve Turing completeness across space, rather than within a single machine.

It is precisely by avoiding the halting problem, simulation errors, and state ambiguity that Bitcoin can scale computation, formalise logic, and model contracts as automata. In this model, not only is everything computable — it is computable verifiably, scalably, and without simulation risk.

Bitcoin is not a toy VM. It is a protocol-layer logic engine. And the Script DFA model is not a weakness — it is the core design feature that makes the entire system secure, scalable, and expressive in the domain of value exchange.

Security by Design — Constrained Expressiveness, Maximal Predictability

I. Whitelist Model of Execution: Only the Explicit Is Permitted

Bitcoin Script follows a whitelist philosophy. Unlike conventional programming languages that allow arbitrary instruction definition and flow control, Bitcoin’s scripting system permits only predefined opcodes, whose behaviours are deterministic, bounded, and constrained. In this model, everything that is not explicitly allowed is forbidden. The language is curated, not expressive for the sake of expressiveness, but precise in the service of predictability and auditability.

Every opcode in Script has an exact stack-based signature: a known number of arguments, a known execution pattern, and a provable result. There is no operator overloading. There are no runtime-generated code blocks. There are no external references. This architectural minimalism ensures that each Script can be reasoned about statically, and its result can be known without execution simulation.

In effect, the Script VM is a symbolic reduction engine, not a computation simulator. This matters. It allows the complete definition of allowable transitions, without the need to trust what might happen during execution. What can be done is what is defined. Nothing else is even syntactically possible. This provides a formal basis for safety.

II. Determinism through Statelessness: Eliminating Race and Reentry

Bitcoin Script executes in an entirely stateless environment. The virtual machine that processes each transaction is born and dies in the context of that transaction's input-validation phase. It has no memory of previous executions, no persistent variables, no hidden registers, and no call stack. It evaluates a single condition: can this output be spent, under the conditions specified by the locking and unlocking scripts?

Because it holds no state, Script is immune to reentrancy. The class of attacks seen in Ethereum contracts—where a contract calls an external contract, which then calls back into the original contract before the first call finishes—cannot exist. The stack is local, scoped, and discarded after use. There is no state to corrupt. There is no control to hijack.

Likewise, race conditions are eliminated. Since every transaction is validated in full as a static object, and because miners choose which transactions to confirm based on independently verifiable criteria, there is no opportunity for parallel interleaving to disrupt logic. This is crucial in financial systems. A transaction is either valid or invalid, regardless of external timing.

III. Oracle Resistance: Script Proves, It Does Not Observe

Bitcoin Script operates without access to external data. It cannot query block metadata, call web APIs, or read random inputs. This is not a limitation. It is a design feature.

Systems that allow arbitrary external data—so-called “oracle-enabled smart contracts”—introduce irreducible trust surfaces. Who provided the data? When? Under what guarantees? What happens if two oracles disagree? These problems are endemic in Ethereum-style platforms, where oracles are the foundation of most contract logic, yet are often implemented as centralised or semi-centralised feeds with opaque failure modes.

Bitcoin’s answer is simple: external truths must be imported through signatures or preimage proofs. If something is to be verified, it must be represented cryptographically. The decision to spend is not based on opinion, timestamp, or changing fact, but on provable knowledge, embedded in the transaction itself. Oracle input becomes simply: can you prove that you know this value, at this moment? And nothing more.

This model means that Script never lies. It cannot say what time it is, what the weather is, or what a stock price is. But it can say: this signature is valid, this hash matches, this preimage was known. It operates in the realm of immutable facts, not inferences.

IV. Constrained Expressiveness: Feature, Not Bug

Traditional computer science defines Turing completeness as the ability to simulate any other machine, given infinite memory and time. But with that power comes undecidability—you cannot know in advance whether a program halts, or whether it behaves as expected in all contexts.

Bitcoin deliberately avoids Turing completeness in single transaction scripts. There is no OP_LOOP, no OP_JUMP, no recursion. This is not a weakness. It is a deliberate rejection of undecidability in favour of provable executability.

In commercial settings, it is not helpful to be able to simulate anything. It is helpful to know exactly what will happen, every time, in every context. Determinism trumps flexibility. Proof trumps simulation. Bitcoin Script is a tool not for expressing arbitrary computation, but for expressing provable state transitions in the domain of value.

And outside of the Script VM, transaction chaining enables full Turing completeness, via conditional graph construction and multi-path signatures. So expressiveness is not eliminated—it is moved to a layer where it can be explicitly modelled and tracked, not buried in arbitrary loops.

V. Proof of Fact, Not Program

Ethereum and other platforms operate as simulation engines. Their contracts model machines: internal state is modified, variables are changed, loops are run. These are procedural machines. Their goal is to recreate a computational process inside the consensus engine. This is not how Bitcoin works.

Bitcoin does not simulate anything. It proves what is already true. A Script does not enact a process. It validates a condition. It is a logical checkpoint. It says: given this input, does the output follow? If yes, the transition occurs. If no, the transition fails. That’s it. No iteration, no mutation, no state simulation.

This approach is not merely simpler. It is more secure. Simulated systems are notoriously fragile. Every state change must be tracked. Every unexpected input must be modelled. Attack surfaces are vast. By contrast, Bitcoin’s model is atomic and unforgeable. Either the claim is valid or it is not. Either the preconditions are satisfied or they aren’t. There is no in-between.

VI. Minimalism as Defence-in-Depth

The security of Script lies not in defensive programming but in attack surface reduction. By limiting the language, Script limits what can go wrong. There are no buffer overflows. No uninitialised memory. No stack smashing. No infinite loops. No deadlocks. No concurrency. No memory management bugs.

This is security by construction. Every component of the system is provable, bounded, and deterministic. That is not just a safe system. It is a model system—a system that demonstrates how constrained design can lead to maximal confidence.

When a transaction is constructed, it is signed over fixed inputs and fixed logic. That logic is verified by all nodes, identically. That verification process is guaranteed to terminate. The inputs and outputs are known. The result is always the same. In other words: Bitcoin Script turns code into law. Not metaphorically, not poetically, but literally. Code is written. The result is fixed. Everyone agrees. The network does not interpret—it evaluates.

VII. The Future Is Bounded, But Unconstrained

While Script is bounded in its per-transaction logic, the full expressive power of Bitcoin lies in the composition of transactions across time and space. With transaction chaining, signature delegation, and externally selected execution paths, Bitcoin achieves total computability through spatial extension, not through unbounded local computation.

This achieves a balance: local safety, global flexibility. Each step is safe. The whole is unbounded. Computation is structured like a decision tree, not like a process simulation. And at each node, a transaction proves that a transition is valid—nothing more, nothing less.

In this way, Bitcoin achieves maximum security through minimal exposure. Its design is not accidental. It is not a scaled-down version of Ethereum. It is the original model for secure, deterministic, contract-based value transfer. And it remains the only one that treats execution not as a game of state, but as a proof of truth.

Script’s Philosophical and Economic Significance

I. The Economy as Assertion: Proof, Not Promise

Bitcoin’s Script is not a tool for speculative execution, simulation, or high-level abstraction. It is an economic predicate logic — a system of verification that affirms whether a condition for payment is met. In this, Script realises a unique form of economic determinism. Every script enforces a claim: if these conditions are true, then value is transferred. The system does not express hope, negotiation, or trust. It expresses only truth — in the form of spendability.

Where other systems strive for expressiveness, Script demands verifiability. The design choice here is neither aesthetic nor technical alone; it is philosophical. It rejects simulation in favour of attestation. Script’s minimal grammar, composed of finite state transitions over the stack, models commerce as a series of binary truths — not as approximations, but as proofs. These proofs are commitments, and their role is not to simulate what might be, but to confirm what is.

II. Minimalism as a Guarantee of Trustlessness

Trustlessness is often misunderstood. It is not born of complexity. It is not achieved through powerful VMs, mutable state machines, or ever-expanding instruction sets. On the contrary, trustlessness emerges precisely from simplicity and constraint.

Bitcoin Script embodies this principle. It avoids recursion, avoids simulation, avoids mutable state, and avoids opcodes that introduce ambiguity, context sensitivity, or race conditions. There is no timing opcode, no stateful access, no introspection of memory. This is not a limitation — it is the reason Script can be trusted.

This is the inverse of smart contract platforms, which often attempt to earn trust by increasing complexity, enabling more features, and hoping that static analysis or gas limits can contain the chaos. In Script, containment is structural. There are no side effects to mitigate because none are possible. The design guarantees determinism, which in turn ensures consensus.

III. Script as a Truth Engine

Bitcoin Script does not model agency. It does not make choices. It does not contain decision logic. It performs no execution of intent. It evaluates whether a statement about value and control is true or false, based on supplied witnesses.

This is why Script is a truth engine, not a will engine. It is not an actor. It is not a participant. It does not simulate the desires of contracting parties. It merely enforces a prior agreement, verifying that a specific statement about control of value is valid.

In this way, Script parallels predicate logic: given a set of premises (the stack), and a list of transformations (opcodes), a single conclusion is reached. The system never acts; it only confirms whether an action can be accepted. The network is not executing logic in the abstract — it is ratifying a proof-of-right, a claim-of-value grounded in verifiable cryptographic conditions.

IV. Temporal Certainty: Automation Through Immutability

Most attempts at automation build complexity. They simulate contracts, build VMs, run continuous processes. But Bitcoin automates by immutability, not simulation. Once a script is committed to a UTXO, it cannot be changed. Once a transaction is broadcast and confirmed, it cannot be reversed. This gives Bitcoin temporal certainty — a form of automated enforcement that requires no active monitor, no executor, no external court.

In this model, Script doesn’t automate processes by running them. It automates their enforcement by ensuring that once committed, the conditions under which value can move are frozen and externally verifiable. It is a static form of automation — deeply reliable, non-interactive, unchanging. Scripts don’t “run” over time; they simply hold until they are provably satisfiable.

This removes the need for reactive monitoring. It enables contracts to be pre-signed, held, distributed, and activated years in the future. It mirrors real-world legal mechanisms: you do not need your lawyer to run your will when you die — it executes because it was pre-committed, witnessed, signed, and held immutable.

V. Economic Layering and Long-Term Value

Bitcoin’s Script is not just a protocol mechanism — it is the basis of a new form of layered economic logic. In this model, complex systems are built not through general-purpose computation but through transactional composition — layering transactions as predicates in time.

This design avoids the pitfalls of gas markets, storage inflation, and oracle dependencies. It scales because it doesn't simulate. It doesn't grow complexity with every new feature. Instead, each transaction is a discrete proof, and each script is a self-contained logical boundary.

This is where long-term value emerges. Not from feature sprawl. Not from emulation of centralised systems. But from compositional certainty. From the fact that every transaction, once written, is immutable. From the guarantee that spending conditions are enforced by logic, not interpreters. From the fact that anyone, at any time, can read a script and understand precisely what it enforces — no dependency, no side channel, no context required.

VI. Bitcoin Script: A Contractual Epistemology

Finally, Script is not merely technical. It is philosophical. It encodes a vision of contracts not as simulation, but as verifiable commitments. It draws a line between “what has happened” and “what could be pretended.” In Script, nothing is assumed, nothing is trusted, and nothing is executed unless all parties have pre-agreed and pre-signed. There is no belief — only proof.

In this way, Script represents a new epistemology for commerce. It says: what we agree upon must be made public. What we claim must be cryptographically demonstrable. What we seek to enforce must be encoded in logic, not in hope. And once encoded, it must never change.

Script is not about programming — it is about proof. Not about computation — about commitment. Not about simulating trust — about removing it entirely.

It is the grammar of truth in an economic system designed to need nothing more.

Conclusion to Chapter 2: The Formal Architecture of Bitcoin Script

Bitcoin Script is not a programming language in the traditional sense. It is a formal system—a logic of transactional finality and assertion. Throughout this chapter, we have traced its architecture not as a means of execution but as a structured validator of claims. It is built to affirm conditions for the transfer of value in a manner that is deterministic, closed, and unambiguous. Each transaction becomes a logical proof, and each script a theorem whose truth is established by witness and verified by the network—not through simulation, but through transformation of state.

The stack-based structure, combined with a bounded opcode set and intentional design constraints, ensures that every script terminates, that every condition is explicitly defined, and that no computation can lead to indeterminacy. Rather than hinder expressive power, this constraint system elevates Bitcoin to the level of composable law. Contracts are encoded not as mutable simulations, but as immutable facts. They are not executed in runtime—they are verified and ratified in broadcast and confirmation.

Temporal anchoring removes reliance on real-time clocks or external state, shifting the burden of decision-making into off-chain logic and on-chain attestation. This creates a system capable of future contingency without centralised arbiters. The chain does not guess—it confirms. It does not model intent—it proves agreement.

Contrary to mistaken claims that Bitcoin Script lacks expressiveness, we have seen that—across time, and with composition—it achieves Turing completeness in aggregate, through conditional path commitment, transaction layering, and branching logic. However, this completeness is not for general computation—it is strictly aligned with bounded economic logic, and with the assurance of finality.

By avoiding loops, recursion, and unbounded state, Script maintains the principle of proof over simulation. There is no memory to alter, no race condition to exploit, and no fallback to oracles. What exists on-chain is immutable, inspectable, and mathematically verifiable by any party, now or in the future. This is not a side effect—it is the purpose.

OP_RETURN, often misused by modern imitators of Bitcoin, is a cautionary example. Script does not exist to carry data without execution. It exists to enforce contracts without ambiguity. The abuse of OP_RETURN highlights the philosophical error of using Bitcoin as a dumb data layer. Script is expressive because it constrains. It speaks with clarity precisely because it is limited.

In sum, Bitcoin Script is the logical framework of an economic revolution: not code-as-contract, but contract-as-proof. Not stateful speculation, but stateless finality. It is the only system where every assertion about control over value is guaranteed to resolve, deterministically, into a binary truth. It is not the simulation of a court. It is the enforcement of an agreement. It is not the expression of hope. It is the commitment of fact. And that, not some abstract idea of "programmability", is what makes it powerful.

The following is the roadmap for what is coming…

Chapter 3: The Architecture of On-Chain Commercial State

Release: Friday 13th

This chapter builds the bridge from Script theory to enterprise system design. Where Chapter 2 dissected Script as a formal machine, Chapter 3 reconstructs Bitcoin (BSV) as a state machine that implements commercial logic using transactions as transitions and chains of proofs. Every section below reflects a rigorously planned logical unit forming a complete and exhaustive summary of how Bitcoin, correctly understood, becomes the substrate for a universal, deterministic, proof-based digital economy.

• Transactions as state transitions, not messages

• UTXO as tokenised state and message simultaneously

• Inputs as verifications; outputs as commitments

• Spending as transition function execution

• Design of chained state: transaction DAGs as history trees

• Comparison with Ethereum's VM: why Script wins in determinism

Chapter 3: The Architecture of On-Chain Commercial State
Release: Friday 13th

---

This chapter transitions from the formal execution model of Bitcoin Script into its role as a foundation for commercial state infrastructure. We move from Script as a predicate logic system to its structural composition as a distributed, cryptographically verifiable, deterministic economic machine. What emerges is not a messaging protocol but a universal ledger of commercial truth, wherein every transaction is a validated state transition, and every output is a cryptographic commitment to future conditions.

---

3.1 — Transactions as State Transitions, Not Messages

• Why Bitcoin is not a messaging system (unlike TCP/IP or API-driven ledgers)

• Transactions as morphisms: input state → validated output state

• Mapping formal system theory: transactions as total functions

• Philosophical contrast: simulation vs. proof

• Concept of compositional determinism: only provable transitions exist

• Preview: macro-opcodes as packaged logic (introduced, not explained yet)

Bitcoin, in its original and legally enforceable implementation (BSV), does not function as a messaging protocol. It is not an API surface. It is not a channel for intent. It is a deterministic state transition system — a formally closed machine that models enterprise and commercial process flows as proof-based transformations of discrete contractual state. This section introduces the fundamental shift in understanding required when transitioning from legacy message-driven architectures to the compositional, automaton-consistent model that Bitcoin provides.

In legacy EDI and modern API stacks, a "transaction" is a term of art: it often refers to a bundle of messages (e.g., EDIFACT documents, HTTP requests) interpreted against mutable state by receiving systems. Messages encode syntactic commands but not provable semantics. The state of the system is derived indirectly, through interpretative middleware, database rollbacks, and context-sensitive control paths. The consequence is architectural: no global transition function exists, and thus, the system as a whole cannot be described as a deterministic automaton.

I. Automata-Theoretic Framing of Bitcoin Transactions

Let us define a commercial protocol not as a software system but as a labelled transition system:

  Σ: Alphabet of valid commercial events
  Q: Set of valid system states
  δ: Deterministic transition function
  q₀ ∈ Q: Initial state
  F ⊆ Q: Accepting (valid terminal) states

A protocol is valid if and only if the application of each event (e.g., an invoice, a shipment, a confirmation) deterministically produces a new state:
  δ: Q × Σ → Q

This is precisely what a Bitcoin transaction does. A transaction T consumes one or more prior UTXOs (state commitments), provides a verifiable witness stack (input), and produces one or more new UTXOs (successor states). Validation is deterministic, non-interactive, and stateless. There is no ambient memory. Every Script execution is a pure function:

  T: σₖ + proof → σₖ₊₁

Where:

• σₖ is a committed economic condition (e.g., payment conditional on multi-sig + delivery window)

• proof is the input ScriptSig satisfying the predicate

• σₖ₊₁ is a new committed state encoded by new ScriptPubKeys

The result is referential transparency. Every commercial state in Bitcoin is the result of a transition that can be independently validated by anyone — not based on API agreements or backend implementation details, but by mathematical reduction of Script conditions to a terminal TRUE or FALSE.

II. Transactions as Morphisms in a Commercial Category

At a higher level of abstraction, we may model the network of valid transitions as a category:

• Objects: UTXO states

• Morphisms: Transactions

• Composition: Transaction chaining

• Identity: Null transition (unspent state)

Each transaction T: A → B maps one state (A) to another (B), provided its unlocking witness is valid. Composability is enforced structurally: outputs from one transaction become inputs to the next. There is no notion of “in-flight” state. State transitions only exist after validation and confirmation. This imposes a temporal consistency that makes rollback, duplication, or forked state impossible by construction.

III. Contrast: Messaging vs. State Execution

Consider an HTTP-based ordering API. A POST to /orders/accept encodes an intent. Whether this intent is acknowledged, committed, or even seen is a matter of server state, middleware, and logging. The transition from “pending” to “accepted” is not enforced — it is implemented. This creates uncertainty.

Bitcoin eliminates this ambiguity. There is no "intent." There is only execution. A transaction either is valid and committed — in which case the state has changed globally — or it is not. It is either mined or it doesn’t exist. The notion of "pending" becomes a local artefact. The system is binary, not narrative.

This shift is profound for commercial systems: Bitcoin does not carry messages; it ratifies facts. This removes the space for interpretation, dispute, and misalignment. The ledger is not a messenger — it is a proof engine.

IV. Transaction Determinism and Closure

Legacy systems typically exhibit open composition: message A leads to process B, unless interrupted by state C, unless overridden by exception D. There is no deterministic closure. Bitcoin, by contrast, is closed under transaction composition. Every valid state arises only from valid transitions. All transitions are irreversible and immutable once confirmed. The structure is formally DAG-complete: the transaction set forms a directed acyclic graph rooted in genesis and growing by confirmed transitions.

Because every transaction is deterministic and context-isolated, validation becomes a local process. This ensures global consensus: no matter which node evaluates the chain, the result is the same. No participant has privileged context. No subsystem can mutate shared state. The global state is what has been provably transformed, not what has been said or requested.

V. Commercial Implication: Enforced Business Logic

When transactions encode commercial logic (e.g., “release goods only if invoice is paid”), Bitcoin ensures that the logic is not advisory — it is executed. Only when a transaction proving payment is valid and confirmed can the delivery token be spent. This inverts the architecture of control. Instead of policy layered atop mutable state, Bitcoin binds action directly to validated transitions.

This property allows Bitcoin to serve not merely as a record of past activity but as the execution substrate of economic coordination. It is a system where commercial agents (enterprises, clients, warehouses) communicate off-chain, but act only when on-chain conditions are met.

---

Conclusion

Bitcoin, as a state transition system, redefines the enterprise architecture of commerce. Its transactions are not messages. They are not instructions. They are not interpreted intentions. Each transaction is a function application, provably transforming one contractual state into another, enforced by the rules of Script and anchored in the consensus DAG. In doing so, Bitcoin provides what legacy systems cannot: deterministic execution, referential transparency, and commercial finality — not through messaging infrastructure, but through computational law.

---

3.2 — UTXO as Tokenised State and Message Simultaneously

• Each UTXO as a dual object: contract + state

• Why ScriptPubKey defines the next legal/economic condition

• UTXOs as closure of economic functions: they declare what must be proven

• UTXOs are messages with cryptographic gates — but they are pull-based not push-based

• Every UTXO is spendable if and only if its Script resolves to TRUE

• UTXO model vs. account model: statelessness vs. mutability

The UTXO (Unspent Transaction Output) model in Bitcoin is often described as a system of digital “coins” or discrete outputs awaiting consumption. But this simplification conceals the deeper automata-theoretic significance of UTXOs: each output is simultaneously a tokenised state and a contractual message, a dual-natured object that both represents the system’s current state and defines the terms under which the next transition may occur.

Unlike a mutable database entry or a ledger balance, a UTXO is a closed functional object: it is stateless in itself yet deterministically activatable under defined conditions. It binds together value, logical constraints, and future expectation in a single, immutable structure. In doing so, it becomes the atomic unit of programmable commercial logic on-chain — not merely a record of what has happened, but a declaration of what must happen next for a valid continuation of system state.

---

I. Formal Definition of UTXO as State Object

Let each UTXO be modelled as a tuple:

  u = (v, Sₚ)

Where:

• v is the committed value (nominal or tokenised asset)

• Sₚ is the script predicate, a function of the form
    Sₚ(w) → {TRUE, FALSE},
    where w is a witness stack submitted in an input attempting to spend u

In automata terms:

• The UTXO u represents a state q ∈ Q, encoded with a symbolic gate

• The system transitions from q to q′ only if a valid witness is provided such that Sₚ(w) = TRUE

The output script is thus not a passive note — it is an executable contract. It defines the totality of acceptable transitions from the current state to any valid future. By design, this predicate is immutable once committed and publicly visible in the blockchain.

---

II. The UTXO as Message: Embedded Future Instruction

Every UTXO carries not only value but also instructions for its own consumption. In other words, it is a tokenised message to the future, binding the recipient not to arbitrary freedom but to a conditional action space. These instructions are not executed when the UTXO is created, but when it is referenced by a future transaction.

This makes every UTXO a form of deferred program, awaiting execution by a valid input. The act of spending the UTXO is not merely a transfer — it is a validation of the encoded contract. No messaging or middleware is needed to determine if the spend is valid. The system itself — via Script — executes the logic and returns a binary outcome.

By this model, a UTXO is a scripted token. It encodes:

• Its intended purpose (e.g., payment, release condition, multi-party approval)

• Its enforcement logic

• Its value constraints

• Its eligibility for future transitions

This makes it both a stateful fact (what has happened and is now committed) and a logical declaration (what conditions must hold for a future spend).

---

III. Compositionality and Isolation: UTXOs as Independent Proof Nodes

Each UTXO is validated in isolation, without dependence on global mutable state. This isolation permits parallel validation, and ensures that Script is side-effect-free. The state machine formed by the UTXO graph is composable: new states are derived only by valid transition of prior states, and all transitions are independent proofs.

Formally, let each transaction T define a mapping:

  T: {u₁, u₂, …, uₙ} × {w₁, w₂, …, wₙ} → {u′₁, u′₂, …, u′ₘ}

Where:

• The inputs uᵢ are UTXOs with Script predicates Sₚᵢ

• The wᵢ are witness stacks

• Each transition is valid iff ∀ᵢ: Sₚᵢ(wᵢ) = TRUE

Because each Sₚᵢ is evaluated independently, this model guarantees determinism and closure: if the inputs are valid and unspent, and the witness stack satisfies the script, then the new UTXOs must be accepted.

This compositional model is structurally equivalent to a DFA with labelled transitions, where each UTXO is a terminal node awaiting reactivation under proven input.

---

IV. Distinction from Accounts: Mutability vs. Assertion

In an account-based model (e.g., Ethereum, SQL-ledgers), balances and contract state are mutated via interpreted commands. A message is sent to a function; the system applies logic and mutates in-memory state. This causes:

• State to depend on prior execution order

• Outputs to vary based on chain position

• Final state to be non-deterministic unless re-executed

In Bitcoin, a UTXO is the state. It cannot be updated. It cannot be partially modified. It is either spent in full under proof, or it remains entirely inert. This ensures:

• All transitions are globally convergent

• Every node evaluates transitions identically

• Consensus is not interpretative — it is logical

Thus, Bitcoin’s UTXO model is not a ledger of balances. It is a ledger of provable commercial assertions, where each assertion must be conclusively fulfilled to be replaced.

---

V. Practical Implication: EDI Instructions as Scripted Outputs

In enterprise terms, a UTXO corresponds to a committed instruction object. For example:

• A warehouse release token (Script requires proof of payment and delivery code)

• A multi-party shipment approval (2-of-3 multisig Script)

• A customs clearance marker (Script time-locked and hash-locked to importer ID)

Each of these is issued as a UTXO and redeemed by supplying the correct witness.

No backend database or API call is required. Every party can independently verify:

• The existence and value of the UTXO

• The logical condition for spending it

• Whether the transaction attempting to spend it meets that condition

The message is no longer an external payload. It is embedded in the system’s state.

---

VI. UTXOs as Global Synchronisation Points

In a distributed supply chain, the coordination of parties often fails because state is synchronised via trust, not proof. The UTXO model resolves this. Each UTXO acts as a universal checkpoint, synchronising state across organisations by providing a single, unambiguous, immutable object representing the current state.

Examples:

• Payment received → emits delivery token

• Token spent → proves collection

• Output received → becomes new claim for return or feedback

Each UTXO becomes a node in a commercial DAG. It serves not as a data row, but as a validated checkpoint, universally recognised and permanently recorded. The flow of goods becomes the flow of validated transitions — no messaging required, no mutual trust required, no sync needed.

---

Conclusion

The UTXO is the irreducible structure of Bitcoin’s commercial architecture. It is both a state object and a tokenised message, a point of synchronisation and a gate of transition. Its script encodes a full legal/economic condition, and its consumption validates fulfilment of that condition. In Bitcoin, state is not a table. It is a graph of proofs. And the UTXO is the unit from which that entire structure is built — immutably, deterministically, and enforceably.

---

3.3 — Inputs as Verifications; Outputs as Commitments

• Inputs are not commands — they are proof submissions

• ScriptSig = witness stack; ScriptPubKey = predicate contract

• Output = declaration of conditional future — input = claim of fulfilment

• A full transaction encodes both an assertion and a transformation

• Economic meaning: transactions are bilateral: I give X if you prove Y

• Legal symmetry: outputs = offer; inputs = acceptance with proof

Bitcoin's transaction structure is deceptively simple: a list of inputs, a list of outputs, a version, and a locktime. But behind this sparse schema lies a formal logic architecture capable of encoding provable commercial processes. In particular, the input and output structure defines a bilateral model: inputs function as cryptographic verifications of prior contractual claims, and outputs function as forward commitments to new conditional states. This section formally dissects this dualism and demonstrates how it maps to a general model of state transitions in deterministic distributed automata.

Whereas legacy EDI and API systems collapse the distinction between claim and commitment—often leading to ambiguity and reversion—Bitcoin transactions enforce a clean separation of responsibility. Every transaction input proves something that has been fulfilled; every transaction output encodes something that is promised, but not yet satisfied.

---

I. Formalising Transaction Inputs: Proof of Past State Satisfaction

Let us begin by considering a transaction T composed of:

• Inputs I = {i₁, i₂, …, iₙ}

• Outputs O = {o₁, o₂, …, oₘ}

Each iₖ references a previous UTXO uₖ = (vₖ, Sₚₖ), which contains:

• A locked value vₖ

• A Script predicate Sₚₖ which must be satisfied

Each input contains:

• The outpoint (reference to uₖ)

• A ScriptSig (a witness stack wₖ) submitted by the party spending it

The Bitcoin protocol mandates that for a transaction to be valid:

  Sₚₖ(wₖ) = TRUE

Thus, the role of the input is not to specify intent or instruction. It is to prove that a prior commitment has been fulfilled under the rules that were previously set. This is validation, not execution.

Inputs are therefore backward-facing attestations. They do not control what the transaction does; they prove that the transaction is allowed to do anything at all. Until a script is proven, no state change can occur. This is the critical distinction: inputs are guardians of the past, not directors of the future.

---

II. Outputs as Forward-Looking Commitments

Now consider the outputs oₗ = (vₗ, Sₚₗ′) of a transaction. Each one defines:

• A value vₗ

• A Script predicate Sₚₗ′, which must be satisfied by any future input that attempts to spend it

These outputs are declarations of conditional control. They state, explicitly and immutably, that some quantity of value will be controllable by anyone who can satisfy Sₚₗ′.

Thus, outputs are forward-facing promises. They define:

• Who may act in the future

• Under what conditions

• With what consequence

Every output encodes the exact logic that must be validated by the next transaction attempting to consume it. The output is not merely an address or a number — it is a programmable commitment to a specific logical condition.

In enterprise terms, this is the equivalent of a contractual clause: “X may occur if and only if Y can be proven.” The system guarantees that no action may occur unless the claim can be validated.

---

III. Inputs and Outputs as Dual Logical Interfaces

From the perspective of automata theory, each transaction functions as a transformation T: σₖ → σₖ₊₁, but more precisely:

• Inputs I provide the proof of satisfaction of the state σₖ

• Outputs O define the conditions that must be satisfied to enter σₖ₊₁

We can model this with the following structure:

Let U be the set of all UTXOs.
Then for T to be valid:

• ∀iₖ ∈ I, there exists uₖ ∈ U such that iₖ proves satisfaction of uₖ’s script

• T destroys {u₁, …, uₙ}, and emits {o₁, …, oₘ} ∈ U with new scripts

So each transaction is a proof-transform:

• It proves the past (via inputs)

• It binds the future (via outputs)

The system thus maintains forward-securing causal integrity. No state appears without a justified predecessor. No commitment exists without an explicitly declared condition.

---

IV. Contrast with Imperative Transaction Systems

In legacy systems, messages may both assert and commit, without separation. For example, an EDI 940 document may request goods to be shipped while also being interpreted by the receiving system as a shipment initiation. This creates ambiguity:

• Was the shipment authorised?

• Was the request valid?

• Did the sender have authority?

Such ambiguity arises because the message is not proven — it is merely formatted correctly.

In Bitcoin, this duality is eliminated. The input must prove that it is entitled to act. The output defines what may happen next. No act of interpretation is required. All terms are explicit, cryptographically committed, and publicly verifiable.

This clean interface — verification vs. commitment — is one of the most powerful features of Bitcoin’s commercial architecture. It makes the protocol legally compatible, logically complete, and technically minimised.

---

V. Enterprise Relevance: Binding Commercial Claims to Contracted Conditions

In supply chain and logistics, the division between verification and commitment maps directly onto real-world roles:

• A warehouse must verify proof-of-payment before releasing goods (input verification)

• A manufacturer may issue delivery tokens to downstream carriers (output commitment)

• A retailer may sign conditional acceptance contracts (output with time or hash lock)

Each actor is operating not as an oracle or interpreter, but as a validator of proofs. The input proves authority; the output defines future obligations. This structure eliminates race conditions, conflicting updates, and data drift. It binds human action to programmable logic, with immutable cryptographic evidence.

---

Conclusion

Bitcoin’s transaction model is a two-sided contract engine: inputs prove that prior obligations have been fulfilled; outputs define new conditional claims that must be satisfied in the future. This division is not merely technical — it is architectural. It ensures that the system can scale commercially, legally, and operationally without ambiguity. In a world of mutable APIs and synthetic ledgers, Bitcoin provides something radically better: a proof-first, commitment-driven, deterministic state machine for commercial coordination.

---

3.4 — Spending as Transition Function Execution

• The act of spending executes the state transition

• Every spend is the application of δ(state, input) → new state

• Script = δ; stack = input; result = transition or failure

• Determinism and atomicity: validation always terminates, no fallback or ambiguity

• Mapping transition logic to automata theory

• Compositionality of spend chains: DAGs as program trees

In the formal architecture of Bitcoin as a transition system for commercial state, the act of spending is not merely a transfer of tokens; it is the execution of a constrained, deterministic function mapping one verified state to another. Each transaction represents a transition between UTXO-defined states, and the validity of that transition is evaluated by executing the concatenated scriptSig and scriptPubKey as a formal logical predicate. This predicate acts as a gate: it either confirms the transition with a final output of TRUE, or rejects it unambiguously. There is no room for interpretive variance. Execution is an act of validation, not computation in the imperative sense.

The model of state is thus formalised as a finite automaton, where UTXOs correspond to states and transactions correspond to state transitions. But unlike the mutable memory model of a Turing machine, Bitcoin uses immutable tapes (transactions) and predicates (scripts) that define exact conditions for transition. Inputs serve as witness-bearing tokens—truth certificates—and outputs encode the next conditionally accessible state. When a spend occurs, it is not a runtime decision but the evaluation of a pre-declared commitment made under strict formal constraints. The system thus enforces referential transparency: no hidden side-effects, no global mutable memory, and no indeterminacy in execution.

From a formal language perspective, this maps directly to a DFA (Deterministic Finite Automaton), where the transaction sequence defines a directed acyclic path through commercially valid states. This is distinct from message-passing systems or imperative APIs that rely on mutable state machines. Bitcoin transitions cannot be “rolled back” or “updated”; once a spend has been accepted and mined, the state transition is locked into history, cryptographically anchored in proof-of-work, and economically enforced through cost. Unlike legacy EDI systems that simulate state via timestamped logs, Bitcoin enforces transition as proof.

Spending, then, becomes the act of evaluating a commitment. The system requires that all inputs resolve to valid logical truths and that all outputs constitute valid postconditions. These truths are encoded not in server logic or middleware state but in the scripts themselves. There is no trusted third party, no adjudication layer, and no arbitrary logic. Instead, there is formal closure: the transaction is its own verifier. The predicates that enforce business rules are encoded directly in script, and execution occurs only when those rules are satisfied.

Moreover, this structure allows for compositional design. Transactions can be chained, branched, and pre-signed to support conditional future paths. Multi-party commercial logic becomes expressible through parallel transitions and pruning of non-selected branches. This, critically, enables modular enterprise design: warehousing, shipping, invoicing, and settlement each occur as distinct state transitions linked only by data integrity and proof, not by inter-process messaging or API orchestration.

Thus, the notion of “spending” in Bitcoin is redefined. It is not payment in the abstract, nor communication in the networked sense. It is proof: the irreversible execution of a verified logical function that transforms commercial state under bounded rules. This is not only secure, scalable, and minimal—it is final.

---

3.5 — Chained State: Transaction DAGs as History Trees

• Bitcoin blockchain as a DAG of transactions (not a linear program)

• Every transaction’s inputs link to earlier states; outputs define future

• Global state reconstructed via graph traversal

• Supply chain and economic state modelling via transaction layering

• DAGs support fork detection, path enumeration, and conflict resolution

• All state is embedded in history: Bitcoin = historical automaton

Bitcoin does not model its global state as a mutable ledger but as a directed acyclic graph (DAG) of transactions. This architecture is not incidental—it is essential. Each transaction in Bitcoin points back to one or more previous outputs (UTXOs) as its inputs, thereby forming a graph in which each node (transaction) depends on earlier nodes for validity and, in turn, offers outputs that may be referenced by future transactions. This structure encodes a historical, non-reversible lineage of economic events, producing not merely a log of activities but a provable state machine whose transitions are cryptographically anchored in time and space.

The fundamental property of a DAG—its acyclicity—ensures that no transaction can depend on itself, directly or indirectly. There is no room for circular logic or re-entrant flows. This enforces determinism, finality, and closure. The Bitcoin blockchain, therefore, is not a linear sequence of state updates but a tree of commercial state rooted in the genesis transaction and branching outward through time. Every transaction is a node; every input is an edge; every output is a potential future node. State is not stored—it is reconstructed by graph traversal.

At any given moment, the set of unspent transaction outputs (UTXOs) defines the system’s current state. But this state is not mutable; it is derivable only from a full traversal of the DAG, verifying each transaction by re-evaluating its scripts and checking its inputs against prior commitments. This makes Bitcoin an explicit historical automaton: the full sequence of transitions defines the machine, and each state exists only in the context of its derivation path. Unlike in imperative systems, where global state is updated and potentially overwritten, Bitcoin’s model is extensional: the entire system is the sum of its validated transitions, and any node can reproduce this state by replaying the chain.

The implications for commercial architecture are profound. Consider a logistics firm with layered operations: order intake, warehousing, dispatch, and settlement. In traditional systems, each component holds a mutable record of state, exposing the entire chain to race conditions, failure propagation, and audit opacity. In Bitcoin, these operations become sequential transitions within a transaction DAG. The order is a UTXO, the dispatch a spend, the settlement another spend. Each step is a transition that consumes prior proof and emits a new commitment. This guarantees that no action can occur without reference to a validated prior condition and that no later step can falsify the past.

This design also enables powerful properties such as fork detection and conflict resolution. If two transactions attempt to spend the same UTXO, they create a fork in the graph. Only one can be confirmed, and the other becomes invalid. This is not resolved by arbitration but by economic consensus—miners accept only one valid path, and the system guarantees that double-spending cannot be accepted by the same chain. Therefore, exclusivity of action is enforced not by trust, policy, or application logic but by structure.

Moreover, Bitcoin’s transaction DAG supports rich modelling of commercial flows. Chains of transactions can encode supply chains, contract lifecycles, manufacturing steps, and multi-party coordination, with each node independently verifiable and globally reproducible. Unlike event logs that simulate flow through mutable databases, Bitcoin embeds flow in its transition architecture. Outputs become checkpoints; their conditions are gates; their spendings are attestations. No central authority needs to validate the chain—validation is consensus-enforced, computation-local, and cryptographically bound.

The architecture thus realises a layered, modular, composable economic machine. Systems do not “communicate” in Bitcoin; they emit and consume verifiable state transitions. Enterprises do not “synchronise”—they reference shared history. The Bitcoin DAG is not a message queue or a replication log—it is a deterministic proof graph in which every edge represents an irreversible economic claim, every node a cryptographic commitment, and every path a valid lineage of commercial action.

In sum, Bitcoin’s use of a DAG transforms the nature of digital state. It renders economic activity not as runtime behaviour but as a declarative series of provable transitions. It permits distributed coordination without centralisation, audit without trust, and composition without risk. Bitcoin does not model the world—it instantiates it. Each transaction is a branch on the tree of commercial truth, and every path through the DAG is a verifiable story of value.

---

3.6 — Contrast with Ethereum: Determinism and Side-Effect Isolation

• Ethereum’s EVM as stateful, mutable, Turing-incomplete VM with gas oracle

• Problems: reentrancy, race conditions, oracle poisoning

• Bitcoin’s stack model as pure function: stateless, deterministic, closed

• Costing: no metered gas pricing → fixed execution cost

• Truth over simulation: Ethereum computes; Bitcoin ratifies

• Legal alignment: Bitcoin scripts can be signed and stored permanently

The foundational divergence between Bitcoin Script and Ethereum’s EVM lies not merely in the syntax of the language or the breadth of operations available, but in their architectural treatment of determinism, side-effects, and the very ontology of state. Ethereum models computation as a mutable virtual machine with global shared memory; Bitcoin models it as a proof evaluator within a stateless, append-only economic automaton. This difference is not cosmetic. It is epistemological.

Ethereum’s core is the Ethereum Virtual Machine (EVM), an account-based, Turing-incomplete interpreter executing imperative code across globally mutable state. Each contract may invoke another, and such invocations can recurse or reenter. This permits arbitrary flow control, delegation, and dynamic state dependencies. However, this also introduces attack surfaces by design: reentrancy vulnerabilities, oracle poisoning, execution races, and inconsistent replayability. A single input may generate different outcomes across time or across nodes, depending on external state, gas conditions, or timing. Gas, in particular, functions as a non-deterministic oracle—a runtime-dependent limiter whose consumption profile changes with node version, network conditions, or internal op-code implementation.

Bitcoin Script, by contrast, is constructed to enforce maximal determinism and eliminate all side-effects. Script does not maintain state beyond the current execution context. It cannot perform loops, recursion, or asynchronous callbacks. There is no inter-contract communication. Each execution is strictly bounded and stateless. The only data it reads are its inputs; the only outcome is binary: pass or fail. The scripting engine is not a simulation engine—it is a predicate logic interpreter. The output of a Script is not a set of variable changes, but a truth value verifying that a given condition has been met.

This confinement is a feature, not a bug. The inability to loop means all scripts are guaranteed to halt. The absence of dynamic calls means the system is closed under verification. The prohibition on state mutation means that no Script can interfere with another or generate non-local consequences. Bitcoin Script’s model is referentially transparent: its result depends only on its inputs, and that result is the same everywhere, every time.

Consider the canonical example of Ethereum’s downfall: the DAO hack. A contract that allowed a withdrawal to be made before the internal balance was updated enabled an attacker to recursively invoke the withdrawal function, draining funds through reentrancy. This is impossible in Bitcoin. A Script can only be executed in full, atomically, and without reentry. No call stack, no callbacks, no nested effects. Either the conditions are met and the UTXO is spent, or they are not and the transaction is invalid. There is no state to exploit because there is no state.

This design paradigm also impacts costing and economic reasoning. Ethereum requires dynamic gas pricing and gas estimation to prevent infinite loops or abuse. Contracts may run out of gas unpredictably, halting mid-execution and creating rollback complexities. Gas is thus not just a resource control mechanism—it is an implicit part of the program logic, undermining clarity and creating non-determinism. Bitcoin’s fixed-cost execution, on the other hand, makes resource usage a function of transaction size and script complexity, not runtime behaviour. Transactions that are valid will always be valid; those that are invalid will never execute. There are no timeouts, no rollbacks, no fallback paths.

From a legal and commercial standpoint, this matters deeply. In Ethereum, contract state at any moment is contingent and revocable. It lives in a database, subject to forks, reorgs, and miner decisions. Bitcoin’s state is cryptographically final. Once a UTXO is spent in a confirmed transaction, that act is immutable. It cannot be reversed, mutated, or rewritten. This creates a level of legal certainty and auditability that no mutable VM can match. Scripts become declarative contracts: “If these conditions are met, the asset is released.” Fulfilment of conditions constitutes execution. There is no gap between contract and action.

Bitcoin also eschews oracles in the traditional sense. Ethereum contracts often rely on external services to import facts from the outside world—market prices, timestamps, shipping updates. These introduce trust dependencies, centralisation vectors, and consensus fragility. Bitcoin’s model assumes off-chain logic and on-chain proof. The world operates independently; parties submit evidence to Script to prove they have satisfied predefined conditions. Oracles, when used, serve only to produce signed statements which are then verified within Script, preserving determinism and minimising trust.

In conclusion, Bitcoin Script is a functionally pure, side-effect-free language designed for cryptographic verifiability and commercial enforcement. Ethereum’s EVM is a general-purpose computational engine built for expressive power at the cost of predictability. Bitcoin prioritises truth over simulation, finality over flexibility, proof over execution. Where Ethereum executes code, Bitcoin ratifies facts. Where Ethereum manages mutable global state, Bitcoin validates composable local claims. In doing so, Bitcoin becomes not a virtual machine, but a global, deterministic truth ledger—immutable, replayable, and judicially meaningful.

---

3.7 — Bitcoin as Economic Automaton

• Bitcoin as a DFA extended over time: each transaction = validated transition

• Global ledger is the composite function: T₁ ◦ T₂ ◦ … ◦ Tₙ

• Finality as execution: no rollback, no side effects, no parallel forks

• Economic logic composed of chain-linked proofs

• Programmability by structural composition, not code mutation

• Automata design in real-world commercial use: customs, warehousing, trade

Bitcoin, correctly interpreted, is not a network of accounts or a mutable ledger of balances—it is a finite-state automaton designed to progress deterministically from one state to the next via formally constrained, cryptographically validated transitions. Each transaction forms a discrete and independent execution step, advancing the commercial state of the system by spending old claims and creating new conditional offers. The automaton is not speculative; it is anchored in economic reality. It processes proofs, not intentions. Its outputs are not messages requesting execution but enforceable commitments bounded by logic.

At its core, this system operates as a DFA—Deterministic Finite Automaton—over a history tree. Each UTXO defines a state, and each valid transaction represents a state transition. These transitions are constrained by Script predicates, which act as transition functions. The DFA’s configuration at any moment is the graph of all unspent outputs; the transition function is applied through the validation of scripts upon attempted spends. In this way, every valid state transition is not merely permitted by the system—it is provable, unambiguous, and irreversible. The result is a global economic machine whose history is not a ledger of changes but a record of immutable proofs.

Bitcoin does not store state in variables, tables, or mutable memory. Instead, state is implied by the set of UTXOs that exist at any given moment. This is a key distinction: Bitcoin does not maintain an internal "world state" as Ethereum does. Rather, it externalises state through the structure of its transaction graph. Each transaction consumes prior outputs and produces new ones. Each of these outputs is an assertion about a future state of affairs: it declares the conditions under which it may be spent, and nothing more. If those conditions are met in a future transaction, the output is consumed; if not, it remains forever unspent.

This automaton is economic in both design and operation. The state transitions it executes are not computationally complex functions but assertions of ownership and conditional transfer. Every transaction embeds a financial logic: "If this key can sign, then these coins may be claimed." More complex logics are possible: escrow, threshold signatures, hash-locks, time-locks. But at every point, the system remains declarative. The script does not say "do this"; it says, "this must be proven true." There is no imperative syntax, no execution path, and no internal memory. The automaton accepts or rejects each proposed state transition based purely on logic and input—no further action is taken.

Critically, each transaction is complete and self-contained. There is no global environment, no session state, no ambient variables. A transaction either satisfies its required predicates and transitions the system, or it fails and is discarded. The automaton has no fallback path and no ambiguity. This is what enables composability: transactions can be chained together indefinitely, with each one referencing outputs created by prior ones, forming a directed acyclic graph. This DAG is not just an implementation artifact—it is the execution trace of the automaton. By traversing the DAG, one can reconstruct the entire economic history of a system, from genesis to present.

Each path through this graph represents a proof chain. If a transaction at the leaf of a path is valid, then every transaction leading to it must also be valid, and every script in that chain must have resolved to true. This gives the Bitcoin automaton a property that no traditional database or virtual machine can offer: structural proof of correctness. Every state transition is cryptographically linked to its predecessors. There is no room for rollback, mutation, or hidden effects. The machine has a single timeline—no parallel branches, no speculative execution, no eventual consistency. It is not eventually correct; it is always correct.

From a systems theory perspective, this is profound. Bitcoin is a compositional economic machine. Each component—each transaction—is a local program, composed only of inputs and scripts. But these local programs can be combined into arbitrarily complex systems. Supply chains, escrow networks, logistics trails, multi-party contracts—all of these can be modelled as chained scripts, each representing a discrete economic event, and each validated independently. There is no need for a central coordinator, no trust in remote APIs or mutable state. The automaton enforces everything.

Finally, this model offers a compelling answer to the question of legal and commercial enforceability. Because each transaction represents a proof, not a command, it can be signed, timestamped, and recorded in a way that courts and institutions can understand. The Bitcoin automaton is a machine of legal determinism. It does not ask whether an event should happen—it verifies whether it already has. It does not simulate economic activity—it ratifies it. The ledger is not a reflection of some external truth; it is the truth, encoded in signatures and hash-locked predicates, embedded forever in the history of transitions.

Bitcoin, then, is not a payment network, not a database, and not a virtual machine. It is a deterministic economic automaton—a machine of irreversible proofs. It executes the logic of commerce, not through imperative code, but through composable declarations. Each declaration forms a node in a graph; each edge is a validated execution. There is no room for ambiguity, no tolerance for inconsistency. In this automaton, truth is not claimed—it is demonstrated, and once demonstrated, cannot be undone.

---

3.8 — Supply Chain State as Formal Execution Graphs

• Every event in a logistics chain as a transaction with inputs/outputs

• Ordering, staging, delivery, handoff → each its own state closure

• Example: staged delivery token modelled as a script condition

• Warehouse and recipient both act as verifiers, not executors

• Human action only valid if on-chain conditions are provably met

• Temporal anchoring of real-world events via transaction commitment

The supply chain is not a metaphor for computation—it is computation. When represented correctly, every stage of the logistical process maps onto a deterministic state transition, each enforced by a transaction on the Bitcoin network. Under this model, commercial logistics ceases to be an opaque, event-driven mess of asynchronous systems and becomes instead a distributed execution graph: an automaton in which each step, each act of handling or approval, is a transition embedded in an immutable history tree. Bitcoin, when correctly understood and applied, is not simply a payment rail. It is the formal infrastructure of truth for global commerce.

In the traditional logistics stack, events such as picking, packing, loading, and delivery are recorded post hoc. These records may be synchronised through shared databases or EDI messages, but the truth of the events is always mediated through institutional trust and fragile interfaces. Worse still, divergence is undetectable until failure. One system may accept that a pallet has shipped; another may not. Disputes emerge not from errors in logic but from the absence of any provable logic in the first place. The problem is not data—it is determinism. Bitcoin solves this.

To represent a logistics chain formally on Bitcoin, one models each real-world event as the execution of a contract. A token representing goods is created in an output, with a ScriptPubKey defining the condition under which it may be spent—perhaps by a signed witness from a specific warehouse terminal, perhaps by satisfying a hashlock associated with a scanned QR code, perhaps gated by a timestamp. This output is then unspent—it is in potential, a claim about the future. When the warehouse operator confirms receipt or dispatch of goods, they submit a transaction that satisfies the Script. This spend is not a request—it is an irreversible execution. The transition has occurred. The automaton has advanced.

Every event in the supply chain—procurement, assembly, transport, customs, delivery—can be modelled in this way. Each action becomes a predicate to be satisfied, a condition to be proven. Each UTXO is a gate; each spend is an assertion of completion. What emerges is a directed acyclic graph of state transitions. This is not a simulation of supply chain events. It is the supply chain, expressed as cryptographically constrained computation. Every state is a node. Every proof is an edge. The result is a fully traversable, fully auditable, fully deterministic economic history.

The power of this model lies in its isolation of validation from execution. The human actors in a logistics process are not executors of global code—they are local witnesses. They act only when the Script conditions are met, and their actions are valid only when embedded in a transaction that satisfies a predicate. This removes trust from the model. A customs authority does not need to trust a shipping company—it needs only to validate that the transaction it sees satisfies the agreed-upon Script. This validation can be done independently, asynchronously, and without prior communication. Every actor is a validator. None are required to be trusted.

More importantly, this structure enables the formal modelling of supply chain state. Because every state is a UTXO, and every transition is a spend, the entire chain becomes a temporal graph. It can be queried, audited, replayed. It is referentially transparent: every output depends solely on its inputs. It is confluent: if two paths result in the same spend, then they are provably equivalent. It is terminating: invalid transactions do not propagate or mutate the system. And it is deterministic: the same input always leads to the same output, provided the Script resolves to true.

This enables the construction of what automata theorists call labelled transition systems. Every node (UTXO) has a label: the script and its metadata. Every edge (transaction) is a transition. States are declared. Preconditions are enforced. Time is linear and monotonic. This is not a toy model. It is an execution graph. And it is live, global, and economically anchored. No other infrastructure—no database, no EDI system, no cloud-hosted ERP—can enforce such constraints without trusted intermediaries. Bitcoin does this inherently.

To illustrate: imagine a shipment that must pass through three facilities—origin warehouse, customs, and recipient. Each facility has a public key and defined logic. The originating transaction defines an output spendable only by the warehouse, subject to possession of a scanning token. The warehouse spends that UTXO and creates a new one for customs, spendable only after a time delay and with a customs signature. Customs spends it, creating the final output for the recipient. The recipient presents a claim, and the Script verifies delivery. The chain is enforced not by communication, but by execution.

Critically, every one of these actions is embedded in Bitcoin’s economic structure. The cost of producing a valid transition is non-zero. The system is secured not just by cryptography, but by capital. Attacking it requires not merely cleverness, but cost. This is not free software. It is a market of truth, where every fact is paid for. This economic constraint is what gives Bitcoin finality. And in the context of supply chains, it transforms every logistical path into a proof of delivery, traceable, irreversible, and cryptographically constrained.

In conclusion, Bitcoin enables the construction of supply chain state machines where every action is a contract, every fulfilment is a transaction, and every transition is globally visible, auditable, and immutable. No longer must enterprises rely on emails, PDFs, or reconciled spreadsheets. They can build execution graphs, where goods flow as tokens, authority is granted by script, and truth is recorded as economic fact. Supply chain management becomes not a process, but a program. Bitcoin is the operating system.

---

3.9 — IP-to-IP Coordination with On-Chain Anchoring

• Communication happens P2P: encrypted, authenticated message flow

• Events (invoice issued, goods picked) exchanged over IP

• But authority to act enforced via script conditions

• Warehouse terminal listens for spendable delivery token

• Pickup → script spend → UTXO burn = finality

• Bifurcation of communication and enforcement solved via Script

Communication in commerce must be real-time, authenticated, and context-aware. But enforcement must be slow, deliberate, and irreversible. This is the fundamental bifurcation that breaks traditional logistics infrastructure: the same system that transmits a message is also expected to enforce its truth. When a user clicks “confirm,” when a warehouse marks “picked,” when a terminal displays “received,” it is assumed that the world has changed. But this is an illusion. Without proof, every update is a rumour. Bitcoin severs this confusion. It divides what is said from what is true. This section formalises that bifurcation.

In standard enterprise resource planning (ERP) and electronic data interchange (EDI) networks, system state is mutated by event messages. A purchase order is issued; a shipment notice is acknowledged; a receipt is confirmed. Each of these is a data packet, often signed and timestamped, but always interpreted by private business logic. These systems are unobservable from outside. They cannot be verified, only believed. Even worse, race conditions and mutability undermine any assumption of synchrony. If two systems disagree about the order of events, the dispute is irresolvable. The root problem is not latency—it is absence of common reference.

Bitcoin does not transmit state—it anchors it. Messages can still be exchanged IP-to-IP, but the actual change of state occurs only when a transaction is submitted, validated, and mined. This creates a clean separation: communication is fast, flexible, and private; validation is slow, fixed, and public. Every commercial actor—warehouse, retailer, supplier—communicates directly, peer to peer. But actions only matter when embedded in a transaction that satisfies a script. This inversion makes Bitcoin not a message bus, but a finality engine.

Concretely, this means the following: a warehouse terminal may receive an IP message indicating that a pallet is ready. That message can contain a pre-signed transaction—one that spends a token representing a right to collect that pallet. The warehouse terminal checks whether the transaction is valid. It does not ask a central server. It does not poll a database. It executes the script locally and deterministically. If the script resolves to true, the pallet is released. If not, no amount of persuasion or override can alter the result. The right to act is enforced cryptographically.

This also decouples coordination from control. A supply chain participant does not require visibility into a partner’s systems to confirm an event. They only require the transaction. The confirmation is the spend. There is no divergence, because there is only one path through the automaton: either the script conditions are met and the token is spent, or they are not and the state remains unchanged. Communication remains off-chain, over IP. But execution—state transition—is on-chain, verifiable, and final.

This has profound implications for logistics, customs, and inventory systems. Traditionally, scanning a barcode is a trigger that sends an API call, which is then interpreted as a state mutation. But such architectures are inherently mutable and unverifiable. With Bitcoin, the barcode encodes a spend condition. Scanning it prepares a transaction. The warehouse terminal submits it, and only if the spend is accepted and mined does the state change. The scan is not a trigger; it is a proof. Every actor retains autonomy. No actor requires trust. Finality is cryptographic, not procedural.

Moreover, because Bitcoin’s validation logic is pure and side-effect free, any node can verify any transaction. This means that even edge devices—handheld scanners, mobile terminals, vehicle-mounted hardware—can act as validators. They do not need to phone home. They do not need to query an API. They can execute script logic directly, determine spendability, and act accordingly. This enables real-time coordination with zero reliance on trusted third parties or centralised infrastructure. It is commercial logic embedded in the fabric of computation itself.

At the protocol level, this reflects a strict separation between two layers: the communication plane and the state layer. The communication plane—IP-to-IP—is arbitrary, unordered, and mutable. It is where intentions are expressed, offers are proposed, confirmations are drafted. But the state layer—the blockchain—is immutable, ordered, and final. It is where commitments are executed, where offers become binding, and where transitions are recorded. Only Bitcoin enforces this split at the cryptographic level. Only Bitcoin guarantees that state cannot be mutated without proof.

It also solves the problem of replay and ambiguity. In legacy systems, messages may be duplicated, misrouted, or lost. In Bitcoin, a UTXO can be spent exactly once. A delivery token, once consumed, cannot be reused. This eliminates classes of error that plague modern logistics systems: double picking, misaligned receipts, duplicated confirmations. Bitcoin does not guess what happened. It encodes it.

This bifurcated model also enables post-facto auditing and verification. Since all state transitions are public, any actor can reconstruct the path taken by a good, a payment, or a contract. This is impossible in EDI or ERP stacks, where records are fragmented across systems, and state is inferred from logs. With Bitcoin, the state is the history. Nothing is inferred. Everything is proven.

In sum, Bitcoin’s architecture decouples communication from control. IP messages express intent. Transactions enforce truth. Every action in a supply chain becomes a binary: provably occurred or provably not. This transforms commerce from a system of best efforts to a system of enforced truth. It enables direct, encrypted, P2P coordination between enterprises without shared infrastructure, while binding their actions to a public, immutable, cryptographically verifiable ledger. It replaces the architecture of trust with the structure of proof.

---

3.10 — Formalising EDI vs. Bitcoin: Semantic Closure and Transition Proofs

• EDI systems validate format (m ∈ F), not truth (⊨ ϕ)

• Bitcoin validates semantic truth: only transitions with satisfied proofs occur

• Legacy systems rely on API logic: undocumented, mutable, unverifiable

• Bitcoin: every transition encoded in chain, enforced by miners

• Transition function is public, deterministic, and replayable

• Referential transparency: output state depends only on known inputs

In traditional EDI (Electronic Data Interchange), the structure of business communication is premised on format validation, not semantic enforcement. Messages are deemed "valid" if they conform to a predefined schema: message m belongs to format set F, i.e., m ∈ F. But conformance to format is not proof of commercial truth. A message stating that goods have shipped may be syntactically perfect yet entirely false. EDI systems validate only form, not fact. In automata terms, they operate on the level of lexing and parsing—never semantic execution.

This distinction is not superficial—it is systemic. Consider a sequence of commercial messages: purchase order (850), shipment notice (940), invoice (810). These are valid within the formal language of EDI. But the system itself is not closed under composition. There exists no deterministic function δ such that δ(qₖ, mₖ) → qₖ₊₁, where qₖ is a commercial state and mₖ is a valid message. That is, no transition function enforces business logic across time. Each message is context-dependent, interpreted differently by each internal system. There is no guarantee that receipt of an invoice implies prior shipment or order. The protocol lacks referential transparency. The outcome of the system depends not only on the message stream but also on mutable, hidden state.

Bitcoin reverses this architecture entirely. It enforces semantic closure. State transitions are not inferred—they are executed. Every commercial event is a transaction that is provably derived from known inputs and whose execution is deterministically verifiable by any observer. Let qₖ be the state encoded in a UTXO, and let tₖ be a transaction that spends qₖ. Then qₖ₊₁ is the state created by tₖ, and this mapping is not a suggestion—it is enforced by the Script attached to qₖ. The transition function is embedded in the protocol. If the conditions are not met, the state cannot advance. This makes Bitcoin a semantic machine.

Formally, Bitcoin transactions are morphisms in a state machine: each one transitions the system from a prior commercial state to a new one, contingent on proof. There is no room for contradiction. A spend either occurs or it does not. A condition is either satisfied or it fails. And this evaluation is immutable once mined. The function f: (qₖ, w) ↦ qₖ₊₁ is public, verifiable, and universal. It accepts a current state and a witness stack, and produces a new state only if Script resolves to TRUE. There is no hidden logic. There are no side effects. Every state transition is deterministic, replayable, and globally consistent.

In contrast, EDI and API-based systems embed transition logic in undocumented, mutable business rules. For a given input message, the resulting state change is an internal decision—often opaque even to participants. There is no guarantee that the same message will yield the same result tomorrow. Worse, these rules are not inspectable. They are compiled into code, distributed across platforms, and updated silently. The function f(m) → Δq is not only undefined—it is unknowable.

This is not merely a technical failing; it has economic and legal consequences. In a dispute, parties must reconstruct intent, infer causality, and resolve ambiguity from a cloud of logs, timestamps, and testimony. Proof collapses into belief. EDI is a system of stories. Bitcoin is a system of facts.

Furthermore, the Bitcoin model supports composability. Every transaction is a programmatic closure over previous state. Complex commercial flows—multi-party delivery, conditional escrow, chained payments—can be encoded as sequences of transactions, each enforcing a semantic boundary. The result is a transaction DAG (directed acyclic graph) that is not just a history, but a computation. Each node is a validated transformation. Each edge is a dependency. The global state of a supply chain becomes a traversable proof tree.

Bitcoin also enables semantic layering. Higher-order business logic—such as order fulfilment, return conditions, or shipment dependencies—can be compiled into Script macros. These macros enforce conditions at the point of execution. They can be audited, signed, and distributed in advance. A manufacturer may encode a refund clause. A warehouse may encode a time-based restriction. All parties verify these clauses locally. None must trust an API. The business logic is enforced by the state machine, not interpreted by applications.

Finally, Bitcoin's semantic closure enables pre-signing. Transactions can be created in advance, contingent on future events. These are not speculative—they are latent proofs. When the event occurs (e.g., a delivery is scanned, a payment is confirmed), the transaction becomes valid and can be broadcast. This separates intent from execution. It allows parties to commit to future actions without revealing sensitive data or relying on runtime conditions. It makes commercial flows asynchronous yet provable.

To conclude: EDI validates the shape of messages. Bitcoin enforces the truth of state transitions. One is a parser. The other is an execution machine. Only Bitcoin ensures that commercial logic is closed, composable, deterministic, and provable. It replaces the brittle architecture of inferred meaning with the solidity of enforced fact. It transforms commerce into computation.

---

3.11 — Commercial and Legal Consequences of State Anchoring

• Immutability = legal certainty: no ambiguity in responsibility or timing

• Pre-signing enables multi-party contracts with time-separated validation

• Every event = provable, timestamped, cryptographic assertion

• Trustless enforcement: no API, no rollback, no mutable database

• Bitcoin contracts survive jurisdiction, litigation, and human failure

• Ledger = global witness with economic cost of falsity

The anchoring of commercial events in Bitcoin’s state machine is not a technical novelty—it is a radical restructuring of legal, economic, and operational truth. Traditional systems rely on mutable databases, human oversight, and legally contestable records. Bitcoin replaces these with immutable, cryptographically enforced execution. Every action taken—every decision, every fulfilment, every failure—can be encoded as a provable, timestamped transaction that forms part of a globally verifiable, unalterable sequence of commercial facts.

Legal certainty arises not from agreement, but from computation. The contract is not what the parties say it is—it is what has been irrevocably committed to the ledger. In this model, commercial responsibility becomes programmable. A seller that signs a transaction with a fulfilment clause cannot later contest it. A buyer who pre-signs a transaction conditional on receipt cannot be compelled to pay unless the script conditions are met. The ambiguity of intent, so often the locus of litigation, is dissolved into boolean logic. Either the transaction is valid or it is not.

This has direct consequences for contract design. Pre-signed transactions represent legal commitments that are activated by proof. Multi-party contracts can be constructed such that parties sign their components in advance, rendering them enforceable only when a precise sequence of events occurs. For example, a shipping firm, a warehouse, and a buyer might each contribute inputs to a delivery contract. Until the delivery is confirmed and signed by the warehouse, the buyer's payment transaction is invalid. Once the condition is met, the payment executes atomically. This enables legal enforceability with asynchronous, distributed participation.

Temporal ordering is enforced by mining and blockchain inclusion. A transaction’s position in the chain gives it a deterministic timestamp with economic cost. There is no "backdating" or selective interpretation. This anchoring of events in a canonical sequence removes much of the ambiguity around when something happened and whether it was properly authorised. It eliminates the grey area that so often leads to litigation. Disputes over sequencing—“I paid before you shipped”—are replaced with proofs: the transaction occurred at height N, with dependencies on M and K.

Jurisdiction is dissolved into protocol. Bitcoin does not care where a transaction was created or by whom. It enforces only that the necessary signatures and scripts are present and valid. This is crucial for cross-border commerce, where different legal systems conflict and enforcement is costly. A contract encoded in Script and mined into a globally recognised ledger requires no further jurisdictional validation. Its enforceability derives not from a court, but from computation. Bitcoin is the court.

Furthermore, Bitcoin’s immutability offers resilience against human and institutional failure. Traditional systems rely on administrator privileges, access logs, and change tracking. All are fallible, vulnerable to corruption or error. Bitcoin removes administrators. No one can modify a mined transaction. No one can retroactively alter terms. No one can "correct" a mistake after the fact. The cost of error is not hidden—it is explicit and borne at the time of transaction creation. This incentivises precision in contract design, and reduces systemic risk from silent data mutation.

Litigation itself transforms. In a Bitcoin-based commercial system, the ledger becomes a witness. Every transaction is a signed statement of action. Every script is a contract clause. Every state transition is enforced. Courts no longer ask "what happened"—they ask "is this script valid, and was it satisfied." Discovery reduces to ledger analysis. Testimony gives way to cryptographic proof. The cost of fraud becomes economic, not procedural.

Moreover, the global nature of Bitcoin ensures uniform enforceability. A transaction broadcast in one country is mined by a global network. Its inclusion in the ledger is not subject to local censorship, nor is its validity determined by regional norms. This universality enables truly international commercial logic, where actors can transact with full assurance that their obligations will be enforced identically regardless of jurisdiction.

Finally, this model supports continuity of obligation. Once encoded, a contract does not disappear. It persists in the ledger, awaiting satisfaction. A condition not met today may still be met tomorrow. This allows for long-term commercial architectures, such as supply chain insurance, escrow with multi-year expiry, or cross-generation asset custody. The script enforces the logic indefinitely. Human memory is no longer a dependency.

In sum, anchoring commercial events in Bitcoin transforms them from suggestions into facts, from contracts into proofs, from legal assertions into executable logic. This shift collapses the distance between commercial design and enforcement. It removes intermediaries. It reduces ambiguity. It encodes responsibility as code and transforms economic action into deterministically computable state transitions. This is not digitisation of commerce—it is its formalisation.

---

3.12 — Compositional Logic: From Predicate Scripts to Complex State Machines

• Macro construction of logic: branchable, conditional, abortable

• Building reusable script templates for shipment, payment, escrow

• Partial completion: chaining through successively spent UTXOs

• Economic determinism: every outcome committed in advance

• Program-by-transaction-chain: Bitcoin as declarative state engine

In the conventional view of programming, complexity arises through layered instruction sets, side-effect-prone memory states, and mutable logic branches. Bitcoin, in contrast, expresses compositional complexity not through dynamic execution, but through the chaining of predicate-based, stateless transitions. The Script language is not Turing-complete within a single transaction by design—but when structured across successive UTXOs, Bitcoin becomes a compositional state machine of arbitrary depth and breadth. The result is a fully deterministic economic automaton whose complexity is architectural rather than computational.

At the core of this model is the principle of predicate chaining: each transaction output encodes a logical condition, and each input provides a proof of satisfaction. This enforces a structure where every unit of state is both contractually defined and computationally verified before it can participate in future transitions. More importantly, this creates a formal grammar for the composition of economic logic, enabling modular construction of commercial protocols from primitive assertions.

Consider the basic construct of conditional value transfer: a ScriptPubKey requiring a digital signature from Alice. This is a minimal predicate—“prove identity by signing with key X.” Extend this by wrapping the same condition within a multi-party clause, such as a threshold multisig, or an AND gate requiring a time lock. Now the logic is: “prove Alice’s signature and a 24-hour delay has passed.” The expressiveness grows combinatorially, but remains closed and decidable. At each step, the Script defines a static logic that must be resolved for state to advance.

Now introduce macro constructions: reusable, encapsulated patterns that abstract common contract forms. For example, a shipment verification macro might define a predicate requiring both warehouse confirmation and buyer signature. This macro can be embedded within higher-order scripts to compose complete supply chain protocols. As Bitcoin script lacks named functions or recursion, macro logic is defined structurally: as a fixed set of opcodes and logical conditions embedded in the Script template. These macros can be signed, versioned, and instantiated repeatedly across chains of UTXOs, creating a composable economic logic library without mutable memory.

The compositionality becomes evident in partial completion: one party signs and commits a transaction, but it only becomes valid when other parties contribute further inputs. This is the essence of asynchronous contract fulfilment. For example, a payment transaction might be constructed with two outputs: one spendable immediately by the shipper upon confirmation, and the other locked until final receipt is proven. Each branch is a forked state path, whose validity is determined by conditions embedded in their respective Scripts. Each Script is a gate. Only the true path is spendable; others remain locked by construction.

As each UTXO can itself be an output of a previous transaction, Bitcoin's state model evolves as a directed acyclic graph of commitments and satisfactions. This transforms the static nature of individual scripts into a dynamic execution graph. There is no global state variable, no virtual machine memory—only the progression of truth as evidenced by spendable conditions. Each spendable output is a realised proof of a prior assertion, and each new output is a claim about future conditions.

Importantly, this architecture enables programmability without reprogrammability. Once published, a Script cannot be changed. This creates economic determinism: all outcomes must be committed in advance. To alter the logic, one must construct a new transaction, not mutate the old one. This property makes Bitcoin uniquely suited to high-stakes commercial systems, where predictability and immutability are more valuable than runtime flexibility.

This contrasts sharply with programmable blockchains like Ethereum, where complexity is built from mutable state, dynamic execution, and developer-owned logic. In Ethereum, contract behaviour can depend on opaque, hard-to-audit internal state transitions, subject to bugs, reentrancy, and unpredictable execution costs. In Bitcoin, the logic is transparent, bounded, and externally verifiable. Each Script is a predicate. Each transaction is a function application. The result is either TRUE or FALSE—there is no side effect, no fallback path, no ambiguity.

The economic implication is profound: Bitcoin enables executable commercial intent. A firm can define its logic not in legal prose or API contracts, but in Script-encoded transactions. These can be audited, signed, pre-validated, and broadcast only when conditions are met. This creates a shift from policy-based enforcement to algorithmic obligation: if the contract is satisfied, it executes; if not, it remains inert. There is no override, no appeal.

From this foundation, complex state machines emerge. A full supply chain—from purchase order to fulfilment, inspection, delivery, payment, and resolution—can be encoded as a graph of linked transactions, each with embedded logic. Each node is a validated transition. Each edge is a proof path. Every actor contributes by satisfying some predicate in the chain. The result is not just a contract—it is a proof-based execution of commercial truth, orchestrated by compositional logic.

In this sense, Bitcoin is not just programmable—it is pre-programmed, deterministically. The computation does not happen at runtime—it happens at design time. Programmers, business analysts, and legal professionals co-author state transitions by defining the Scripts that encode their logic. The network, through miners, enforces these transitions with cryptographic finality.

Thus, compositional logic in Bitcoin is a redefinition of what software means in a commercial context. It is not code that runs on a server—it is logic that executes through consensus. It is not simulation—it is commitment. And it is not mutable—it is a declaration of intent rendered in digital stone.

Compositional Execution and Path-Pruned Automata: Constructing Dynamic State Forests in Bitcoin

Bitcoin, properly understood, expresses complexity not through runtime mutation but through the architectural composition of transactions as predicates over discrete states. In this extension, we push beyond the conceptual frame of compositional logic and examine the technical construction of execution graphs—what we term transactional automata—wherein multiple transaction chains represent diverging conditional futures. These chains exist in a superspace of latent commitments, with each path representing an exclusive, prunable future. This is not just abstract theory: it is a deterministic model of executable state forests, built from signed, unsent transactions, structurally akin to non-binary Merkle trees but functionally realised through compositional state transitions.

Let us define the basic primitives:

• Let U₀ be a UTXO at genesis of this automaton.

• Let each transaction Tᵢⱼ represent a transition from input Uᵢ to a new set of outputs {Uⱼ₀, Uⱼ₁, ..., Uⱼₖ}.

• Each output Uⱼₖ embeds a Script predicate Pⱼₖ that governs its spendability.

• A transaction chain is a sequence of (signed) transactions that consume and produce UTXOs along a defined path.

• Crucially, multiple transactions may be constructed to consume the same input Uᵢ, forming mutually exclusive transitions.

This forms a branching execution graph: from each committed UTXO, we may construct N signed transaction candidates. Each is valid under the consensus rules, but only one may ultimately be mined. The others, by definition, become pruned paths—legally constructed but invalidated by the selection of an exclusive branch.

⬛ Construction of a Dynamic State Forest

We begin with U₀. Suppose U₀ encodes a Script such that the spender must provide a valid signature and a declared delivery status. Now suppose the delivery status can be one of four enumerated types: {ARRIVED, MISSING, DAMAGED, DELAYED}. We pre-construct four candidate transactions {T₁₀, T₁₁, T₁₂, T₁₃}, each of which spends U₀ and claims a different delivery state, embedded into ScriptSig as a parameter.

Each transaction T₁ₓ, for x ∈ {0, 1, 2, 3}, commits to a unique future. The act of mining one causes the others to become forever invalid. The other paths do not “fail”; they become provably unspendable—since the input U₀ is now consumed. This is not branching logic in the traditional computational sense—it is an exclusive future selector backed by economic finality. In automata terms, we model this as:

 δ(U₀, T₁₀) → U₁₀
 δ(U₀, T₁₁) → U₁₁
 δ(U₀, T₁₂) → U₁₂
 δ(U₀, T₁₃) → U₁₃

where δ is the deterministic transition function defined by Script evaluation and transaction context. Once one δ is executed by mining, all other δ paths are pruned.

This builds a non-binary tree: each UTXO node may have multiple child edges, each one defined by a pre-signed transaction. Unlike Merkle trees, which are strictly binary with fixed hashing structure, this automaton is executional—its branches are not hash links but full transition definitions, each containing predicate logic and proof payloads. It is a state transition DAG with exclusive branching and irreversible pruning.

⬛ Example: Conditional Payment and Shipment Paths

Suppose a seller wants to define multiple potential future states depending on the condition of goods upon arrival. They construct a sequence:

• U₀: payment locked until shipment condition declared.

• T₁₀: “Goods arrived OK” → unlock 100% to seller.

• T₁₁: “Goods damaged” → unlock 50% to seller, 50% refunded to buyer.

• T₁₂: “Goods delayed” → delay window unlock; time lock enforced.

• T₁₃: “Goods missing” → full refund to buyer.

Each T₁ₓ is constructed, signed, and held in cold storage. Only one is broadcast, depending on the actual condition. Once any is mined, the others are invalid due to double-spending of U₀. We now compose forward:

• U₁₀ → T₂₀₀: seller claims funds.

• U₁₁ → T₂₁₀ and T₂₁₁: seller and buyer claim respective halves.

• U₁₂ → T₂₂₀: after delay expiry, seller may claim reduced funds.

• U₁₃ → T₂₃₀: buyer claims full refund.

Each UTXO at layer 2 continues the structure: more pre-signed transactions for handling receipt confirmation, tax clearance, inventory updates, etc. These form a depth-n DAG, pruned at each stage by the mining of exclusive predecessors.

⬛ Structural Analogy: Multi-Way Merkle Execution Trees

While Merkle trees use cryptographic commitments to data in a binary branching model (left/right), the execution forest here is a state-committed automaton, where each transition is a node, and the branches are not binary but arbitrary in fan-out. Moreover:

• In a Merkle tree: leaf nodes contain data; intermediate nodes hash children.

• In this automaton: all nodes are transactions; children are constrained transitions from parent UTXOs.

• A Merkle proof verifies inclusion; a transaction proof verifies execution.

Thus, selecting path 1 → 2 → 4 → 5 → 3 prunes all alternatives at each stage. In the fourth layer, if you select the third path (say, T₄₃), then all other candidates for that parent input are invalidated. Each path commits forward deterministically. You do not “cancel” or “delete” branches—they are made unexecutable by the spend of their parent.

Unlike Merkle structures, this DAG encodes meaning and consequence. Each pruned path corresponds to an alternative future that is provably not the world that came to pass. This gives the Bitcoin graph narrative power: it is a historical automaton. Not only do we prove what did happen; we prove what could not have happened.

⬛ Technical Realisation: Unsigned and Signed Transactions

Crucially, many of these branches are built off-chain, using transactions that are fully signed and valid but not yet submitted. These are stored, sequenced, and selectively broadcast depending on real-world events. This is compositional programming by transaction orchestration. It offers:

• Asynchronous control: each party signs only when its predicate is satisfied.

• Atomicity: broadcast one branch; all others are invalidated.

• Replay resistance: once a path is chosen and mined, no other is possible.

To support this system in practice:

• Transactions must be signed and hashed in advance.

• All input scripts must encode exclusive conditions.

• UTXOs must be unambiguous: if multiple transactions claim one input, the first mined transaction wins.

• Pre-signing requires full deterministic knowledge of all inputs, outputs, and Scripts.

• Complex contract templates are instantiated by parameter substitution (like macros) and then signed.

⬛ Theoretical Frame: Pruned Execution Trees as State Machines

This graph is a path-restricted automaton. Let each node be a state qᵢ, each transaction be a labelled transition δ(qᵢ, a) → qⱼ, and the input symbol a be the transaction payload and satisfaction proof. Then:

• The automaton is nondeterministic in construction but deterministic in execution: multiple δ(qᵢ, a₁) → qⱼ₁, δ(qᵢ, a₂) → qⱼ₂ may exist, but only one will be realised due to mining.

• Pruned paths represent unreachable states, in the formal language sense.

• Once a path is realised, the automaton commits to that branch permanently.

This structure is closed under prefix, as each partial path represents a valid transaction history. It is not closed under composition, because future transactions must respect the output states of the past. However, it is closed under concatenation of validated paths.

We conclude: this execution forest is not Turing complete, but it is computationally universal within its own substrate. That is, any commercial process that can be encoded as a finite set of preconditions, branching predicates, and verifiable outputs can be modelled as a state-pruned Bitcoin transaction DAG.

⬛ Implications

This model introduces a shift in commercial system architecture:

• Logic is encoded before execution, not at runtime.

• Side effects are replaced with mutually exclusive, committed branches.

• Business logic becomes formal state grammar, where each transaction is a sentence.

• Participants do not send messages—they publish satisfactions.

In Bitcoin, we do not simulate. We prove. We do not program by mutation. We architect by structure. The result is an economic grammar: provable, declarative, and executed with finality.

---

3.13 — Failure Modes of Traditional Logistics (Case Study Response)

• The “double pick” scenario: when paper processes create unrecoverable loss

• Warehouse acts without updated payment truth → duplication

• Bitcoin remedy: only one path is spendable — all others provably locked

• Losses prevented by enforced exclusivity, not policy

• Real-world divergence solved by immutable state transition logic

In legacy logistics systems, operational reliability is not enforced by mathematics but by process compliance. This produces systemic fragility. Errors occur not because the actors are malicious, but because the protocol does not prevent conflicting actions from being treated as simultaneously valid. One of the most telling examples is the “double pick” scenario: the inadvertent release of the same shipment multiple times, typically due to timing mismatches or conflicting data between systems. In traditional enterprise resource planning (ERP) and warehouse management systems (WMS), the possibility of double execution is a structural failure embedded into the very nature of the architecture—mutable databases, asynchronous communication, and no cryptographic finality.

A typical manifestation begins with a payment or invoice being registered in the customer relationship management (CRM) system or the billing layer. This triggers a pick request downstream to the warehouse. However, due to latency, failure of API callbacks, or retry logic at the application layer, the same pick request is received multiple times—or worse, a delay in processing leads to a second manual release. From the warehouse's perspective, each instruction appears valid. There is no authoritative source that disallows execution. No spend condition is ever provably consumed—because there is no concept of finality embedded in the structure.

Let us reconstruct this scenario using the model of on-chain state and contrast the two.

---

⏹ Traditional Failure Mode: No Exclusive State Ownership

• Actor A pays invoice via system API. The record updates, but no state is irreversibly consumed.

• Actor B (Warehouse) receives a pick instruction via message queue or API callback.

• A second instruction, triggered either by human error or automated retry, is received later.

• The system cannot cryptographically prove that the first instruction was fulfilled, because all state is mutable. So it executes both.

The result: two shipments go out. Reconciliation is manual. Loss is not provable in real time and is often discovered post-facto.

---

✅ Bitcoin Model: Single Path Spend, Irreversible and Provable

Now, replace this architecture with Bitcoin's Script-based control. The warehouse holds a UTXO representing the right to pick a shipment, issued by the client as a conditional output. The UTXO contains a Script that requires proof of pick-up (e.g., scanned delivery token, signed confirmation) and a unique customer identifier.

• UTXO: PICK_TOKEN issued to warehouse address, containing script: "Deliver if signed by warehouse key AND delivery token matches purchase order".

• Spend attempt 1: valid signature and token. Transaction is broadcast and mined.

• Spend attempt 2: same UTXO referenced → transaction invalid due to double spend.

The very structure prevents multiple executions. There is no possible valid chain state in which both transactions can be confirmed. The warehouse cannot release the shipment twice—not by policy, but by cryptographic law.

---

🧮 Automaton Model of Resolution

Let S₀ be the initial state: shipment available, UTXO unspent.
Let T₁ be the first delivery confirmation transaction.
Let T₂ be a second attempt to deliver the same goods.

Then:

• δ(S₀, T₁) → S₁: goods delivered, token consumed.

• δ(S₁, T₂) is undefined: the UTXO does not exist in S₁.

No fork of the state machine can permit both T₁ and T₂. If T₁ is mined, T₂ is invalid. If T₂ is mined first, T₁ becomes invalid. This is not error recovery—it is error prevention through exclusive state transition.

---

📊 Real-World Cost Model

In legacy systems:

• Errors → chargebacks, restocking fees, legal liability.

• Failures → data mismatch, audit exposure.

• Resolution → manual, delayed, prone to dispute.

In Bitcoin-anchored systems:

• Errors are mathematically impossible when transitions are well-formed.

• Costs are known in advance: the cost of publishing a transaction.

• Disputes are reduced to proof of spendability, a binary condition.

---

⚙ Why Traditional Systems Cannot Guarantee This

Centralised logistics systems:

• Are mutable: state can be overwritten, not spent.

• Are not compositional: no deterministic transition function exists.

• Are not closed: external effects (human action, retries, delays) mutate internal state without constraint.

• Are opaque: no global view of state; no third-party provability.

Bitcoin transactions:

• Are immutable once mined.

• Enforce exclusivity via UTXO consumption.

• Create a ledger of actions that cannot be re-executed.

• Provide timestamped, cryptographic evidence of execution.

---

📌 Conclusion: Exclusivity as Execution

The double-pick problem is not solved by better API retries or audit logs. It is solved by rearchitecting the execution model itself. Bitcoin replaces database mutation with deterministic transition. The warehouse no longer “trusts” that it should ship—it proves it has the right. The right exists exactly once. Once exercised, it is burned.

In this model, there are no ghost states. Every transition path either occurs or is provably blocked. The supply chain becomes not just digitally recorded—but mathematically defined.

---

3.14 — Linking Commercial Actors with Bitcoin State

• Client systems, warehouse terminals, and logistics platforms as Script-aware nodes

• P2P message exchange confirms intent; Script enforces truth

• Example: customer presents pre-signed transaction, warehouse releases goods

• Every system is a validator: no actor required to trust upstream state

• Supply chains become distributed automata: inputs, scripts, transitions

The architectural leap from enterprise APIs and message queues to on-chain contract enforcement introduces not merely a technological change but a fundamental realignment of responsibility. Traditional commercial actors—clients, suppliers, warehouses, terminals—function as semi-autonomous silos linked by mutable data flows. They exchange intent through messages and enforce agreements via implicit trust in systemic coherence. The shift to Bitcoin's UTXO-based execution model dissolves this assumption and replaces it with a structure in which only objectively provable actions are permitted, and all authority flows from verifiable ownership of spendable state.

To implement this, each participant becomes a Script-aware actor. That is: each commercial system becomes a state machine interpreter, not merely a messaging node. Rather than trust a shared database or coordinated API logic, each party observes and participates in the network by listening for the emergence of spendable UTXOs tied to its own action space. This enforces a distributed model of coordination, wherein each actor only accepts responsibility if and when the state indicates it is valid to do so.

---

🧾 Concrete Example: Client-to-Warehouse Shipment Release

• Client system constructs a transaction T₀ whose output represents a shipment request: a token bound to a unique purchase order and warehouse identity.

• Script encodes preconditions: “Warehouse W may release goods if signed token matches PO123, delivery address verified, and timestamp exceeds Friday 09:00 UTC”.

• Client signs and sends this transaction to the warehouse via IP-to-IP communication, but does not yet broadcast it to the chain.

• Warehouse system verifies the transaction's structure, validates the signature, and prepares to act—but does not yet release.

• At pickup time, Warehouse signs the transaction, completes any required fields (e.g., delivery staff ID), and broadcasts it to the network.

• Once mined, the output is burned and replaced by a “goods released” UTXO confirming finality.

The release of goods is not triggered by a mutable database entry or API acknowledgement. It is enforced cryptographically: goods can be released if and only if the Script is provably satisfied, and the transaction is confirmed on-chain.

---

🔐 Commercial Actors as Validators, Not Executors

This paradigm shift reframes what it means to “participate” in a commercial system:

• Clients do not issue commands; they construct contracts (ScriptPubKeys) and commit to payment conditions.

• Warehouses do not execute blindly; they verify spendability, perform local validation, and assert proof through ScriptSig.

• Logistics coordinators become transaction assemblers, handling chained state across handoffs.

• Auditors do not reconcile databases; they enumerate transaction chains and derive state proofs from the DAG.

All actors thus shift from imperative command structures to functional participation models, in which state changes only when evidence is sufficient and preconditions are met.

---

🏗 Architecture of Integration

To enable this model, commercial infrastructure must evolve:

1. Script-Aware Interfaces
   ERP, CRM, and WMS systems must include libraries for constructing and evaluating Bitcoin Scripts. These need not expose end-users to Script directly, but must embed Script logic as transaction templates in business processes.

2. UTXO State Observers
   Each actor runs a listener module: a node-linked or indexer-linked engine that watches for UTXOs matching relevant keys or scripts. These determine when actions become authorised.

3. P2P Message Exchange
   Pre-broadcast transactions, signed by clients, are sent directly to partners over authenticated IP channels. These transactions are offers, which become enforceable once countersigned and mined.

4. Action Gates
   Physical terminals (e.g., dockside gates, warehouse dispatch tools) are programmed to act only when a spendable UTXO exists. This enforces cryptographic gating of real-world execution.

---

🧠 Human and Machine Cohesion

Critically, the system is human-operable but machine-enforced. The client may choose to draft, sign, and send a transaction, but no human can override the Script once it has been committed. Similarly, warehouse staff cannot override the gate—the spendability of the UTXO is the sole determinant of action.

This model removes ambiguity, circumvents dispute, and eliminates race conditions. There is no case in which both parties “believe” something happened differently. What occurred is what was mined.

---

🌍 Emergent Property: Global Commercial Determinism

When each actor becomes a validator of its own state conditions, and all transitions are globally visible, the system acquires deterministic structure:

• Each event is a verifiable state change.

• Each state is the only path available given prior actions.

• Each action is gated by satisfaction of encoded conditions.

Thus, the entire commercial domain becomes an interlocking automaton—a system of distributed, cryptographically bound actors who together enact a globally visible, dispute-resistant economy.

This is not just an improvement on logistics—it is a new computational substrate for commerce itself.

Case Study: Commercial Actor Integration Through On-Chain Predicate Enforcement

This section presents a technical case study demonstrating how distinct commercial actors—client systems, logistics terminals, and warehouse interfaces—are coordinated through pre-committed transaction construction and Script-based state enforcement. The objective is to show in exacting technical detail how human decision-making and physical logistics are subordinated to deterministic, immutable state machines enforced on-chain. All transitions must be provable, spendable, and enforced without off-chain assumptions, middleware, or mutable databases.

There are no oracles. There is no "timestamp validator." The logic must be self-contained, fully expressible in Script, and enforced solely by the validity of a spend transaction. All other considerations are irrelevant.

---

Scenario: Multi-Stage Goods Release Across Distributed Facilities

Three commercial actors are involved:

• Retail Client System (C) initiating a delivery contract;

• Distribution Warehouse Terminal (W) responsible for inventory;

• Carrier Dispatch Node (D) that finalises physical pickup.

The goal is to enforce a shipment that only occurs if (1) the goods are properly prepared by W, and (2) the dispatch occurs under a signed confirmation from D. No trust exists between C, W, or D. All coordination must occur through chained transaction logic, never through messaging.

---

Step 1: Client Constructs Root Contract Output

Client C generates a transaction T₀ with a single output:

• Value: nominal delivery fee;

• ScriptPubKey:

IF

<pubkey_W> CHECKSIGVERIFY

<commitment_hash> EQUALVERIFY

<pubkey_D> CHECKSIG

ELSE

<refund_pubkey_C> CHECKSIG

ENDIF

This defines two branches:

• If W and D sign, and the commitment hash matches a predefined delivery bundle, the funds can be claimed;

• Otherwise, after W fails to act, client C may reclaim funds.

However, no refund path is enforced here. There is no timeout. If W fails to act, the money is forever inaccessible unless the refund path is coded and signed ex ante. The system enforces responsibility through design.

---

Step 2: W Constructs Pre-Signed Delivery Preparation Transaction

W assembles but does not broadcast transaction T₁ that spends T₀. The ScriptSig must satisfy the IF-branch:

• Push W’s signature;

• Push the hash of the committed delivery bundle (e.g., hash of product IDs, quantities, timestamp);

• Leave D’s signature blank.

W shares this partially signed transaction with D directly over an authenticated channel.

At this point, the delivery cannot be executed. D must append their signature.

---

Step 3: Dispatch Node Verifies and Completes Transaction

Upon arrival at W’s loading dock, D’s terminal reads the QR code containing the pre-signed transaction. It verifies:

• The delivery bundle hash matches the manifest physically present;

• W’s signature is valid;

• C’s contract is correctly represented in the script.

If valid, D appends its own signature, producing a completed transaction T₁'.

Once broadcast and mined, the funds are released to D, the contract is marked as settled, and the UTXO is consumed.

---

Resulting State Chain

• T₀ = Initial contract creation.

• T₁ (partially signed) = W confirms preparation.

• T₁' (fully signed) = D accepts and executes.

Each state is a node in a verifiable graph. All paths not taken—e.g., refund by C, or alternate carriers—are permanently pruned upon spend.

---

State Diagram Construction

This interaction forms a non-binary branching structure:

             T₀
              │
   ┌───┴────────────┐
 T₁(w)                                   Tₓ(refund)
   │
   └─ T₁'(w + d)

Where Tₓ is a possible refund path only valid if pre-signed and only spendable if the original UTXO remains unspent.

All other theoretical transitions—unsigned, unverifiable, or uncommitted—are invalid in practice and mathematically impossible to enact.

---

Example of Path Pruning and Commitment Trees

Let’s extend the model to a 5-stage chain:

• T₀: client creates root delivery contract.

• T₁₀: warehouse A accepts preparation.

• T₂₀: carrier D1 accepts pickup.

• T₃₀: customs clear item.

• T₄₀: final delivery accepted.

Now consider alternate routes:

• T₁₁: warehouse B offers alternate preparation.

• T₂₁: carrier D2 available.

• T₄₂: package rejected by recipient.

The entire state space becomes a branching transition tree:

         T₀
        /  \
     T₁₀   T₁₁
     |       |
   T₂₀     T₂₁
     |       |
   T₃₀     T₃₁
     |       |
   T₄₀     T₄₂

Once any full chain (e.g. T₀ → T₁₀ → T₂₀ → T₃₀ → T₄₀) is broadcast and mined, all other branches are forever invalidated. No other UTXO remains spendable. The system enforces exclusive resolution by cryptographic proof and economic finality.

---

Merkle-like Execution Trees

Though this structure resembles a Merkle tree, it is not binary. Branching can be arbitrarily complex and depends solely on business logic. Unlike a Merkle tree that aggregates hashes, this system commits to possible paths through signed transaction graphs.

Each signed-but-unbroadcast transaction becomes a latent leaf node. Once any parent is spent, all alternate children are pruned.

This forms a cryptographic execution tree where every choice collapses future options. There is no rollback. Each spend is a final, exclusive commitment.

---

Consequence

This architecture renders it physically impossible for:

• A carrier to release goods without both W and D cryptographically committing;

• A warehouse to act without the correct token;

• A client to double-fund or reassign delivery after execution.

Every actor participates only if and when the predicate contract permits it. The system is closed, deterministic, and complete.

This is not conditional logic simulated in a VM.

This is enforced logic instantiated through irreversible transactions. Reality is not a state in memory—it is a committed chain of validated decisions.

---

3.15 — Chapter Conclusion: Bitcoin as the Substrate of Commercial Verifiability

• Bitcoin (BSV) is not a database or VM — it is a state machine

• Every output is a claim, every input is a proof

• Transactions are not communications — they are executions

• Script binds human action to immutable digital consequences

• Commercial logic, encoded permanently, enforceable globally

• This is not a simulation — it is reality made computable

The preceding sections form a unified technical architecture: a complete reconstitution of commerce as a deterministic state machine, not merely facilitated by Bitcoin, but executed through it. The result is not a platform. It is not a framework. It is a cryptographically enforced system of economic truth, where action is possible only if proof exists and where state exists only through validated transition.

Each transaction is not a message but a transformation — a realisation of a conditional commitment predeclared by one party and activated through demonstration by another. Outputs are not values. They are encoded invitations to specific outcomes, each governed by contract logic expressible in Script and validated through consumption. Inputs are not requests — they are mathematical submissions of sufficiency, demonstrable by stack execution and committed through miner consensus.

There is no external database. There is no API authority. No system outside the ledger can override what the ledger enforces. What is written into the chain is not a record; it is a cryptographic verdict: a binding statement of fact determined by proof and finalised through immutable economic cost.

This model is not hypothetical. Every example — from layered supply chain predicates to multistage transaction graphs — demonstrates how commerce becomes a chain of conditionals, with execution governed by contract and state resolved only through validation. There are no trusted third parties. There is no middleware. Every actor, whether a warehouse scanner or ERP backend, becomes a validator node in a broader automaton whose global state is encoded in UTXOs, whose program logic is Script, and whose transitions are final.

This is the end of ambiguity. The separation between “business intent” and “technical execution” is eliminated. No actor may act unless the conditions are met; no condition may be declared unless it is provable; and no proof may exist unless it survives the scrutiny of execution.

In this model, commerce becomes computable. Not simulated. Not synchronised. Not processed. Computable.

This is Bitcoin — not as payment — but as the underlying machine of law, contract, and commercial finality. There is no need to trust, wait, or guess. The system is complete. The system is public. The system is true.

Case Study: Automaton-Based Commercial Execution in Warehousing and Logistics Using Scripted Bitcoin Transactions

In this case study, we construct a full-stack commercial execution pipeline over Bitcoin Script, reifying a supply chain not as a coordination protocol but as a deterministic automaton. We show, through a real-world analogue, how inventory state, actor permissions, and terminal events (e.g., physical delivery) are encoded, enforced, and pruned as cryptographically committed paths on-chain. The environment is a multi-actor warehousing system with a distributor, a third-party logistics provider (3PL), an internal warehouse manager, and an external retailer. The entire process chain is modelled as a DAG of unspent and partially-signed transactions, executed through Script without recourse to off-ledger arbitration or mutable state.

---

Setup: Economic Topology and Actors as Validators

The network topology consists of five nodes, each corresponding to a participant in the commercial state machine:

1. Distributor Node (D) – entity holding economic authority over goods and initiator of shipment.

2. 3PL Node (L) – manages transit between warehouse and retail end.

3. Warehouse Terminal (W) – script-aware validator of inventory dispatch.

4. Retail Receiver (R) – endpoint of delivery, and final UTXO claimant.

5. Audit Observer (A) – optional node replicating state for regulatory or assurance purposes.

These are not separate trust domains. All parties are Script-aware and run deterministic stack evaluation locally. The only common source of truth is the transaction graph. No central clock. No message bus. No API calls. Only a shared model of economic transitions enforced by predicate validation.

---

Phase I: Construction of Conditional Commitments

Let us assume the distributor wants to initiate a delivery of 10,000 units of Product X to the retailer. Instead of pushing a message to the 3PL and waiting for confirmation, the distributor constructs a pre-signed set of transactions forming a transaction tree:

• T₀: Initial output of 10,000-token UTXO locked to the condition:

▸ "Spendable only if signed by W and L and accompanied by a hash-preimage proving an external delivery manifest."

This output represents a contractual assertion — not that the goods will be shipped, but that a proof could be provided such that they can be released.

• T₁ₐ, T₁_b, ..., T₁ₙ: Branches representing discrete shipping options, e.g., via Carrier A, B, or C. Each is locked to mutually exclusive delivery script conditions.

Each of these is a potential future, encoded but not yet published. All are signed by D. Some are co-signed by L. Only one will be made valid — and only once its Script condition is met.

---

Phase II: Inventory Encoding as Automaton State

The warehouse system receives the transaction tree and loads it into its internal validator, a software module that:

• Parses each output script.

• Builds a finite state representation of shipment permutations.

• Anchors each output UTXO to internal inventory state, i.e., units available, loading capacity, time constraints.

This warehouse validator does not act. It merely transforms the transaction tree into an automaton over potential outcomes. The terminal states are leaf transactions where:

1. All required signatures are present.

2. A delivery token is included matching the expected item hash.

3. The stack evaluates to TRUE.

Only such terminal transactions are broadcast and mined. Others are cryptographically pruned by non-execution.

---

Phase III: Execution and Path Pruning

Suppose the distributor and 3PL mutually agree on Carrier B. The warehouse validates T₁_b, signs it, and constructs T₂, a terminal spend of the conditional UTXO to the retailer’s key, encoded as:

▸ "Spendable by R if timestamped proof of delivery at location Y before 2025-08-01T10:00Z is provided."

Upon this transaction being broadcast and mined, the entire alternate tree of T₁ₐ, T₁_c, ... is pruned. Not by deletion, but by loss of spendability. The moment T₁_b is executed, all sibling transactions are provably invalid, as their shared ancestor UTXO is consumed.

This is not a rollback. It is automaton convergence. The active state path advances along the selected branch. The others are retained for audit but cannot be resurrected. The system's transition function is:

 δ: (UTXO₀, proof₁) → UTXO₁

 δ: (UTXO₁, proof₂) → UTXO₂

Where each δ is fully transparent, replayable, and bounded.

---

Structural Analysis: Multibranch Execution as Generalised Non-Binary Tree

Unlike a Merkle tree, which encodes past data with fixed fan-out and binary branching, the transaction automaton is a non-binary, dynamically constructed conditional tree of future potentialities. Each branch corresponds to a predeclared but unexecuted transaction. Some branches may themselves spawn further sub-branches with their own script conditions, recursively.

Let us represent a simplified transition chain:

• T₀ → T₁₀ → T₂₀ → T₃₁ (executed)

• T₀ → T₁₁ → T₂₄ (pruned)

• T₀ → T₁₂ (never signed)

Once T₃₁ is confirmed, the entire subtree rooted in T₁₁ and T₁₂ is cryptographically dead. It is not garbage-collected — it is preserved as negated potential. This provides perfect forward determinism and perfect backward auditability.

---

Warehousing Logic as Temporal State Encoding

The physical warehouse integrates this automaton through programmable inventory locking. No physical goods are moved unless the terminal transaction exists. The loading dock is connected to a Script-aware system which:

• Validates the conditional output.

• Confirms delivery criteria match manifest.

• Submits signature + proof payload.

• Triggers spend and physical release.

No operator discretion. No off-chain messaging. The loading dock acts only when the ledger proves permission.

---

Business Significance: Deterministic Fulfilment Infrastructure

This architecture eliminates race conditions, misdelivery, or double-pick scenarios. There is no way for two warehouse terminals to independently authorise different paths. If a terminal signs one path and broadcasts it, the rest are irrevocably invalid.

This system also allows for staged delivery, escrow with proofs, time-delayed release, and auditable fallback recovery by chaining macro-script branches and recording all conditional outputs prior to spend.

The economic logic is precise:

• Offers are encoded in outputs.

• Acceptance is encoded in input satisfaction.

• Performance is verified through stack execution.

• Transition is finalised through mining.

Each actor’s rights, obligations, and authority are encoded in key signatures and script predicates. There are no oracles, no gas estimators, no side-effect simulators. Only proof.

---

Conclusion: Historical Automaton as Commercial Execution Layer

The warehousing and logistics pipeline described here is not a conceptual model. It is an instantiation of Bitcoin’s true design: a deterministic, stack-based automaton where economic action is permitted only via verifiable predicates.

This is not “smart contracts” in the vanity-scripting, race-prone, EVM-based sense. It is not data storage. It is not a timestamp service. It is a formal system of truth in which commercial history is not recorded but executed, and where execution cannot be faked, reverted, or selectively ignored.

No rollback. No reversion. No forgiveness.

Only state. Only proof. Only truth.

⚙️ PART II — DESIGNING SCRIPTED EDI: SYSTEM MODEL AND CANON

While the full outline of Part 1 will be made publicly available, encompassing the foundational logic, architecture, and capabilities of Bitcoin Script within the context of commercial automation, Part 2 will initially be offered under a subscriber model. This second part will delve into implementation-level detail, advanced patterns, and system integration strategies, with eventual public release scheduled for a later phase. At a further stage, the complete work—including both parts—will be prepared and published in formal book format through the Ring, ensuring longevity and citability. This will be accompanied by a comprehensive, line-by-line breakdown and interpretative analysis of the original Bitcoin white paper, placing it in the full technical, philosophical, and legal context intended but often misunderstood.

Chapter 4 coming by the 20th June 2025…